题目内容
【题目】如图所示：质量为M=0.8kg的小车有半径R=1m的1/4光滑圆轨道BC和长为0.5m的水平轨道AB，小车静止于光滑的水平面上，质量为m=0.2kg的小物块（可看成质点）以水平向右的初速度v0在A点滑上小车。已知物块与小车的水平面间的动摩擦因数为
=0.5，g=10m/s2。求：
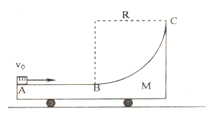
(l）若小车固定，物块刚好滑到小车上的C点，则物块的初速度v0多大？
(2)若小车自由，物块仍以v0滑上小车，物块相对水平面AB所能到达的最大高度是多少？
(3）在（2）的情况下，分析说明，物块最终能否停在小车上，若能确定位置，若不能，求出两者分离时的速度。（取
)
【答案】（1）5m/s；（2）0.75m；（3）1.7m/s
【解析】（1）由能量守恒： 
mv02=fL+mgR
摩擦力 
而FN=mg
解得： v0=5m/s
(2) 物块与车水平方向动量守恒：mv0=(m+M)v
解得： v=1m/s
物块与车系统能量守恒： 
mv02=μmgL+mgh+
(m+M)v2
解得最大高度：h=0.75m
(3)若停在小车上有： 
mv02- 
(m+M)v2=μmgs
s=2m>2L
所以不会停在小车上，即两者分离；设两者分离时m的速度v1，车的速度v2，物块与车水平方向动量守恒：mv0=mv1+Mv2
物块与车系统能量守恒：μmg2L=
mv02- 
mv12- 
Mv22
解得 v1 =﹣1.8m/s 说明分离时m的速度方向与v0方向相反
车的速度 v2 =1.7m/s
练习册系列答案
相关题目
