题目内容
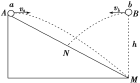
【题目】“嫦娥四号”探测器经过约110小时奔月飞行,到达月球附近,成功实施近月制动,完成“太空刹车”,被月球捕获,顺利进入环月轨道,经过几次变轨修正后,“嫦娥四号” 落月前绕月球做周期为T、轨道半径为 r的匀速圆周运动。2019年1月3日上午10点26分,“嫦娥四号”探测器成功着陆在月球背面,“嫦娥四号”探测器在降落到月球表面前经过几次弹跳才停下来。若某次落到月球表面弹起后,到达最高点时距离月球表面的高度为 h,相对接触点的水平位移为x,已知月球是半径为r0的均匀球体,引力常量为G。求:

(1)月球的质量;
(2)月球表面的重力加速度;
(3)“嫦娥四号”探测器该次落到月球表面的速度。
【答案】(1)![]() (2)
(2)![]() (3)
(3)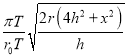
【解析】
(1)以 M表示月球的质量,m表示“嫦娥四号”探测器的质量,由万有引力定律和牛顿第二定律有
![]()
解得
![]() 。
。
(2)以g'表示月球表面附近的重力加速度,m'表示月球表面处某一物体的质量,由重力等于万有引力得
m'g'=G![]()
解得:
g'=![]() 。
。
(3)用v 表示“嫦娥四号”探测器该次落到月球表面的速度,其竖直分速度大小为v1,水平分速度大小为v2,则有
v1=![]()
v2=![]() =x
=x![]()
合速度
v=![]()
解得:
v=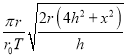

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目