题目内容
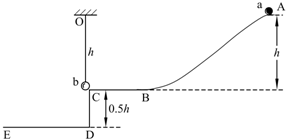
如图,小球a、b质量均为m,b球用长h的细绳(承受最大拉力为2.8mg)悬挂于水平轨道BC(距地高0.5h)的出口C处.a球从距BC高h的A处由静止释放后,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起.试问:
(1)a与b球碰前瞬间的速度大小?
(2)a、b两球碰后,细绳是否会断裂?
(3)若细绳断裂,小球在DE水平地面上的落点距C的水平距离是多少?若细绳不断裂,小球最高将摆多高?
(1)a与b球碰前瞬间的速度大小?
(2)a、b两球碰后,细绳是否会断裂?
(3)若细绳断裂,小球在DE水平地面上的落点距C的水平距离是多少?若细绳不断裂,小球最高将摆多高?

(1)设a球经C点时速度为vC,则由机械能守恒定律得
mgh=
m
解得vC=
,即a与b球碰前的速度为
(2)设b球碰后的速度为v,由动量守恒定律得
mvC=(m+m)v
故v=
vC=
小球被细绳悬挂绕O摆动时,若细绳拉力为T,则由牛顿第二定律有
T-2mg=2m
解得T=3mg,则有T>2.8mg,细绳会断裂,小球做平抛运动.
(3)设平抛的时间为t,则依据平抛运动的规律得
0.5h=
gt2(
得t=
故落点距C的水平距离为S=vt=
×
=
h
即小球最终落到地面距C水平距离是
h.
答:
(1)a与b球碰前瞬间的速度大小是
.
(2)a、b两球碰后,细绳会断裂.
(3)细绳断裂,小球在DE水平地面上的落点距C的水平距离是
h.
mgh=
| 1 |
| 2 |
| v | 2C |
解得vC=
| 2gh |
| 2gh |
(2)设b球碰后的速度为v,由动量守恒定律得
mvC=(m+m)v
故v=
| 1 |
| 2 |
| 1 |
| 2 |
| 2gh |
小球被细绳悬挂绕O摆动时,若细绳拉力为T,则由牛顿第二定律有
T-2mg=2m
| v2 |
| h |
解得T=3mg,则有T>2.8mg,细绳会断裂,小球做平抛运动.
(3)设平抛的时间为t,则依据平抛运动的规律得
0.5h=
| 1 |
| 2 |
得t=
|
故落点距C的水平距离为S=vt=
| 1 |
| 2 |
| 2gh |
|
| ||
| 2 |
即小球最终落到地面距C水平距离是
| ||
| 2 |
答:
(1)a与b球碰前瞬间的速度大小是
| 2gh |
(2)a、b两球碰后,细绳会断裂.
(3)细绳断裂,小球在DE水平地面上的落点距C的水平距离是
| ||
| 2 |

练习册系列答案
相关题目