题目内容
如图16-1所示,一个连同装备总质量为M=100千克的宇航员,
在距离飞船为S=45米与飞船处于相地静止状态。宇航员背着
装有质量为m0=0.5千克氧气的贮氧筒,可以将氧气以V=50米/秒的喷咀喷出。为了安全返回飞船,必须向返回的相反方向喷出适量的氧,同时保留一部分氧供途中呼吸,且宇航员的耗氧率为 R=2.5×10-4千克/秒。
试计算:
小题1:(1)喷氧量应控制在什么范围? 返回所需的最长和最短时间是多少?
小题2:(2)为了使总耗氧量最低,应一次喷出多少氧? 返回时间又是多少?

在距离飞船为S=45米与飞船处于相地静止状态。宇航员背着
装有质量为m0=0.5千克氧气的贮氧筒,可以将氧气以V=50米/秒的喷咀喷出。为了安全返回飞船,必须向返回的相反方向喷出适量的氧,同时保留一部分氧供途中呼吸,且宇航员的耗氧率为 R=2.5×10-4千克/秒。
试计算:
小题1:(1)喷氧量应控制在什么范围? 返回所需的最长和最短时间是多少?
小题2:(2)为了使总耗氧量最低,应一次喷出多少氧? 返回时间又是多少?
小题1:允许的最大和最小喷氧量为:
mmax=0.45千克,mmin=0.05千克。
返回的最短和最长时间为:tmin=
 =200秒,tmax=
=200秒,tmax=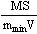 =1800秒
=1800秒小题2:返回飞船的总耗氧量可表示为:△M=m+Rt=(MS/vt)+Rt
因为MS/vt与Rt之积为常量,且当两数相等时其和最小,即总耗氧量最低,
据:MS/vt=Rt,所以相应返回时间为:t=
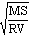 =600秒
=600秒相应的喷氧量应为:m=Rt=0.15千克。
一般飞船沿椭圆轨道运动,不是惯性参照系。但是在一段很短的圆弧上,可以认为飞船作匀速直线运动,是惯性参照系。
小题1:(1)设有质量为m的氧气,以速度v相对喷咀,即宇航员喷出,且宇航员获得相对于飞船为V的速度,据动量守恒定律:mv-MV=0
则宇航员返回飞船所需的时间为:t=S/V=MS/mv
而安全返回的临界条件为:m+Rt=m0,以t=MS/mv代入上式,得:m2v-m0vm+RMS=0,m=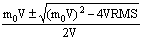
把m0、v、R、M、S代入上式可得允许的最大和最小喷氧量为:
mmax=0.45千克,mmin=0.05千克。
返回的最短和最长时间为:tmin= =200秒,tmax=
=200秒,tmax=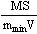 =1800秒
=1800秒
小题2:(2)返回飞船的总耗氧量可表示为:△M=m+Rt=(MS/vt)+Rt
因为MS/vt与Rt之积为常量,且当两数相等时其和最小,即总耗氧量最低,
据:MS/vt=Rt,所以相应返回时间为:t=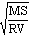 =600秒
=600秒
相应的喷氧量应为:m=Rt=0.15千克。
小题1:(1)设有质量为m的氧气,以速度v相对喷咀,即宇航员喷出,且宇航员获得相对于飞船为V的速度,据动量守恒定律:mv-MV=0
则宇航员返回飞船所需的时间为:t=S/V=MS/mv
而安全返回的临界条件为:m+Rt=m0,以t=MS/mv代入上式,得:m2v-m0vm+RMS=0,m=
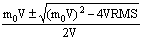
把m0、v、R、M、S代入上式可得允许的最大和最小喷氧量为:
mmax=0.45千克,mmin=0.05千克。
返回的最短和最长时间为:tmin=
 =200秒,tmax=
=200秒,tmax=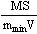 =1800秒
=1800秒小题2:(2)返回飞船的总耗氧量可表示为:△M=m+Rt=(MS/vt)+Rt
因为MS/vt与Rt之积为常量,且当两数相等时其和最小,即总耗氧量最低,
据:MS/vt=Rt,所以相应返回时间为:t=
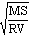 =600秒
=600秒相应的喷氧量应为:m=Rt=0.15千克。

练习册系列答案
相关题目
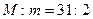 )
)