题目内容
【题目】如图，MN、PQ两条平行的粗糙金属轨道与水平面成θ=37°角，轨距为L=1m，质量为m=0.6kg的金属杆ab水平放置在轨道上，其阻值r=0.1Ω．空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度为B=0.5T．P、M间接有R1=4Ω的电阻，Q、N间接有R2=6Ω的电阻．杆与轨道间的动摩擦因数为μ=0.5，若轨道足够长且电阻不计，现从静止释放ab，当金属杆ab运动的速度为10m/s时，求：（重力加速度g=10m/s2 ， sin37°=0.6，cos37°=0.8）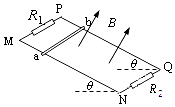
（1）金属杆ab之间的电压；
（2）金属杆ab运动的加速度大小．
（3）金属杆ab在下滑过程中的最大速度．
【答案】
（1）解：当金属杆ab运动的速度为10m/s时，
ab杆产生的感应电动势为：E=BLv=0.5×1×10V=5V，
R1与R2并联的总电阻为：R= 
= 
=2.4Ω，
流过ab杆的电流为：I= 
=2A
金属杆ab之间的电压为：U=IR=2×2.4V=4.8V．
答：金属杆ab之间的电压为4.8V；
（2）解：杆ab受到的安培力为：F安=BIL=0.5×2×1N=1N
对杆ab分析，根据牛顿第二定律得：mgsinθ﹣μmgcosθ﹣F安=ma
代入数据解得金属杆ab运动的加速度大小为：a=0.33m/s2．
答：金属杆ab运动的加速度大小为0.33m/s2．
（3）解：设金属杆的最大速度为v，则有：mgsinθ﹣μmgcosθ﹣BLI=0
I= 
，
代入数据解得：v=12m/s
答：金属杆ab运动的最大速度大小为12m/s．
【解析】（1）根据切割产生的感应电动势公式求出ab杆产生的电动势大小，结合串并联电路的特点求出总电阻，根据闭合电路欧姆定律求出电流，从而得出金属杆ab之间的电压．（2）根据安培力公式求出ab杆所受的安培力，结合牛顿第二定律求出金属杆的加速度大小．（3）当金属杆所受的合力为零时，速度最大，结合平衡，以及安培力公式、切割产生的感应电动势公式等求出最大速度．
【考点精析】解答此题的关键在于理解电磁感应与电路的相关知识，掌握用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向；画等效电路；运用全电路欧姆定律，串并联电路性质，电功率等公式联立求解，以及对电磁感应与力学的理解，了解用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向；求回路中电流强度；分析研究导体受力情况（包含安培力，用左手定则确定其方向）；列动力学方程或平衡方程求解．
