题目内容
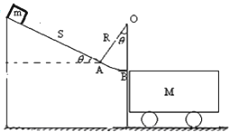
【题目】如图所示,一质量为m=1kg的滑块从倾角为θ=37°的斜面上自静止开始滑下,滑行距离s=9m后进入半径为R=9m的光滑圆弧AB,其圆心角也为θ=37°,然后水平滑上与平台等高的小车。已知小车质量为M=5kg,滑块与斜面及小车表面的动摩擦因数![]() ,地面光滑且小车足够长,取g=10m/s2(sin37°=0.6,cos37°=0.8)求:
,地面光滑且小车足够长,取g=10m/s2(sin37°=0.6,cos37°=0.8)求:
(1)滑块在斜面上的滑行时间![]()
(2)滑块滑到B点时的速度![]()
(3)当小车开始匀速运动时,滑块在车上滑行的距离![]()
【答案】(1)3s(2)![]() (3)6m
(3)6m
【解析】
(1)根据牛顿第二定律及匀变速直线运动的规律即可求出时间及到达A的速度;
(2)根据动能定理求出滑块滑到B点时的速度;
(3)根据动量守恒定律求解共同速度,再根据能量关系求解滑行距离。
(1)滑块在斜面上的滑行加速度a,由牛顿第二定律,有![]() ,
,
解得:a=2m/s2,
根据位移时间关系可得:![]() ,解得
,解得![]() ;
;
滑块在A点的速度![]()
(2)滑块在圆弧AB上运动过程,由动能定理:![]() ,
,
解得![]() ;
;
(3)设二者相对静止时的速度为v,根据动量守恒定律可得:![]() ,
,
解得:![]() ;
;
根据能量关系可得:![]() ,
,
解得:![]() 。
。

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目