题目内容
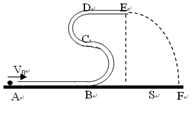
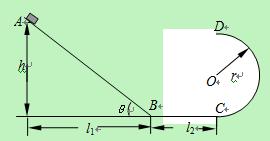
(10分)如图所示,两个半圆形的光滑细管道(管道内径远小于半圆形半径)在竖直平面内交叠,组成“S”字形通道。大半圆BC的半径R=0.9m,小半圆CD的半径r=0.7m。在“S”字形通道底部B连结一水平粗糙的细直管AB。一质量m=0.18kg的小球(可视为质点)从A点以V0=12m/s的速度向右进入直管道,经t1="0.5s" 到达B点,在刚到达半圆轨道B点时,对B点的压力为NB=21.8N。(取重力加速度g=10m/s2)求:
(1)小球在B点的速度VB及小球与AB轨道的动摩擦因数m ?
(2)小球到达“S”字形通道的顶点D后,又经水平粗糙的细直管DE,从E点水平抛出,其水平射程S=3.2m。小球在E点的速度VE为多少?
(3)求小球在到达C点后的瞬间,小球受到轨道的弹力大小为多少?方向如何?

(1)小球在B点的速度VB及小球与AB轨道的动摩擦因数m ?
(2)小球到达“S”字形通道的顶点D后,又经水平粗糙的细直管DE,从E点水平抛出,其水平射程S=3.2m。小球在E点的速度VE为多少?
(3)求小球在到达C点后的瞬间,小球受到轨道的弹力大小为多少?方向如何?
(1)m=0.4(2)VE="S/" t=4m/s(3) NC="18.25N" 方向向上
(10分)
(1)根据牛顿第二定律有NB-mg=mVB2/R
VB="10m/s " --------------------- (2分)
a=(V0-VB)/t=4m/s2
m mg="m" a a =mg m="0.4" -----------(2分)
(2)H=2R+2r=3.2m
t=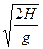 VE="S/" t="4m/s" -----------------------(3分)
VE="S/" t="4m/s" -----------------------(3分)
(3)NC- mg=mVC2/r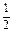 m VB2="2mg" R+
m VB2="2mg" R+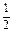 m VC2
m VC2
NC="18.25N" 方向向上 ------------------------(3分)
(1)根据牛顿第二定律有NB-mg=mVB2/R
VB="10m/s " --------------------- (2分)
a=(V0-VB)/t=4m/s2
m mg="m" a a =mg m="0.4" -----------(2分)
(2)H=2R+2r=3.2m
t=
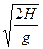 VE="S/" t="4m/s" -----------------------(3分)
VE="S/" t="4m/s" -----------------------(3分)(3)NC- mg=mVC2/r
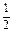 m VB2="2mg" R+
m VB2="2mg" R+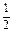 m VC2
m VC2NC="18.25N" 方向向上 ------------------------(3分)

练习册系列答案
相关题目
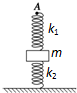
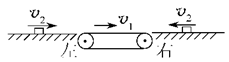

 共同向右运动。已知木板与墙碰撞后立即反向且速度大小不变,木块不会滑离木板和碰到墙。求木板在第二次碰墙后的运动过程中,木板速度为零时木块的速度。
共同向右运动。已知木板与墙碰撞后立即反向且速度大小不变,木块不会滑离木板和碰到墙。求木板在第二次碰墙后的运动过程中,木板速度为零时木块的速度。