题目内容
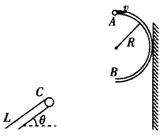
如图所示,有一半径为R=0.30 m的光滑半圆形细管AB,将其固定在竖直墙面并使B端切线水平,一个可视为质点的质量为0.50 kg的小物体优由细管上端沿A点切线方向进入细管,从B点以速度vB=4.0 m/s飞出后,恰好能从一倾角为θ=37°的倾斜传送带顶端C无碰撞的滑上传送带。已知传送带长度为L=2.75 m(图中只画出了传送带的部分示意图),物体与传送带之间的动摩擦因数为μ=0.50(取sin37°=0.60,cos37°=0.80,g=10 m/s2,不计空气阻力,不考虑半圆形管AB的内径)。
(1)求物体在A点时的速度大小及对轨道的压力大小与方向;
(2)若传送带以v1=2.5 m/s顺时针匀速转动,求物体从C到底端的过程中,由于摩擦而产生的热量Q;
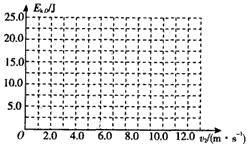
(3)若传送带逆时针匀速转动且速度为v2,物体到达底端时动能为EkD,请在下面的坐标系中画出EkD随v2变化的关系图线,要求在坐标轴上标出图线关键点的坐标值,并说明是什么曲线。(不要求写出计算过程,只按画出的图线评分)
(1)求物体在A点时的速度大小及对轨道的压力大小与方向;
(2)若传送带以v1=2.5 m/s顺时针匀速转动,求物体从C到底端的过程中,由于摩擦而产生的热量Q;
(3)若传送带逆时针匀速转动且速度为v2,物体到达底端时动能为EkD,请在下面的坐标系中画出EkD随v2变化的关系图线,要求在坐标轴上标出图线关键点的坐标值,并说明是什么曲线。(不要求写出计算过程,只按画出的图线评分)
解:(1)由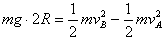 ,得vA=2 m/s
,得vA=2 m/s
设物体在A点所受轨道作用力为FA
则由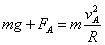 ,可得
,可得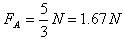
由牛顿第三定律得物体在A点时对轨道的压力大小为1.67 N,方向为竖直向上
(2)物体落到传送带顶端C时的速度大小为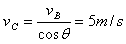
传送带顺时针匀速转动时,对物体施加的摩擦力沿传送带上表面向上
则由mg(sinθ-μcosθ) =ma1,可得物体匀加速运动的加速度大小为a1=2 m/s2
由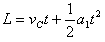 ,得物体从C到底端的时间t=0.5 s
,得物体从C到底端的时间t=0.5 s
此过程中,由于摩擦而产生的热量为Q=f·(L+s带)=μmgcosθ·(L+v1t)=8 J
(3)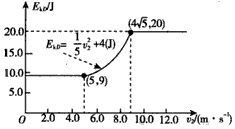
Ⅰ、中间段曲线及起始点正确1分,方程正确1分(方程可以不写在图线上);
Ⅱ、v2≤5 m/s时,EkD=9 J或在图上标出点(5,9),且图线正确1分;
Ⅲ、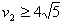 m/s时,EkD=20 J或在图上标出点,且图线正确1分;
m/s时,EkD=20 J或在图上标出点,且图线正确1分;
分情况讨论;
①当v2≤vC=5 m/s时,物体一直以a1=2 m/s2匀加速下滑,到达D点时的速度大小为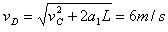 ,即EkD=
,即EkD=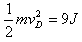
②若物体所受传送带摩擦力沿传送带上表面向下
则物体加速度大小为a2=g(sinθ+μcosθ) =10 m/s2
若一直以a2匀加速,则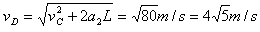
所以:当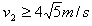 时,
时,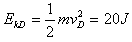
③当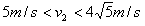 时,物体先以a2=10 m/s2匀加速,与传送带速度相同后,再以a1=2 m/s2匀加速运动到D端
时,物体先以a2=10 m/s2匀加速,与传送带速度相同后,再以a1=2 m/s2匀加速运动到D端
则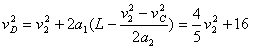
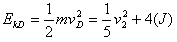
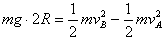 ,得vA=2 m/s
,得vA=2 m/s 设物体在A点所受轨道作用力为FA
则由
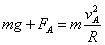 ,可得
,可得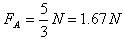
由牛顿第三定律得物体在A点时对轨道的压力大小为1.67 N,方向为竖直向上
(2)物体落到传送带顶端C时的速度大小为
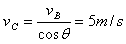
传送带顺时针匀速转动时,对物体施加的摩擦力沿传送带上表面向上
则由mg(sinθ-μcosθ) =ma1,可得物体匀加速运动的加速度大小为a1=2 m/s2
由
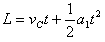 ,得物体从C到底端的时间t=0.5 s
,得物体从C到底端的时间t=0.5 s 此过程中,由于摩擦而产生的热量为Q=f·(L+s带)=μmgcosθ·(L+v1t)=8 J
(3)

Ⅰ、中间段曲线及起始点正确1分,方程正确1分(方程可以不写在图线上);
Ⅱ、v2≤5 m/s时,EkD=9 J或在图上标出点(5,9),且图线正确1分;
Ⅲ、
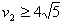 m/s时,EkD=20 J或在图上标出点,且图线正确1分;
m/s时,EkD=20 J或在图上标出点,且图线正确1分;分情况讨论;
①当v2≤vC=5 m/s时,物体一直以a1=2 m/s2匀加速下滑,到达D点时的速度大小为
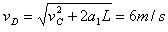 ,即EkD=
,即EkD=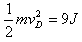
②若物体所受传送带摩擦力沿传送带上表面向下
则物体加速度大小为a2=g(sinθ+μcosθ) =10 m/s2
若一直以a2匀加速,则
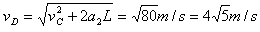
所以:当
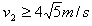 时,
时,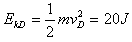
③当
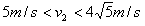 时,物体先以a2=10 m/s2匀加速,与传送带速度相同后,再以a1=2 m/s2匀加速运动到D端
时,物体先以a2=10 m/s2匀加速,与传送带速度相同后,再以a1=2 m/s2匀加速运动到D端则
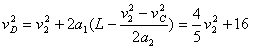
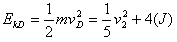

练习册系列答案
相关题目
 如图所示,有一半径为R质量为m的半球形凹槽P,放在光滑的水平地面上,一面紧靠在光滑的墙壁上,在槽口正上方某处有一质量为m的小球,由静止释放,落下后可沿光滑的球面滑下.试问:
如图所示,有一半径为R质量为m的半球形凹槽P,放在光滑的水平地面上,一面紧靠在光滑的墙壁上,在槽口正上方某处有一质量为m的小球,由静止释放,落下后可沿光滑的球面滑下.试问: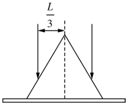 (2012?湖南模拟)桌面上有一玻璃圆锥,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,此三角形的边长为L,如图所示,有一半径为
(2012?湖南模拟)桌面上有一玻璃圆锥,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,此三角形的边长为L,如图所示,有一半径为 如图所示,有一半径为r的导电圆环处于磁感应强度为B的匀强磁场中,磁场方向垂直纸面向里且与圆环平面垂直,圆环的电阻为R.若磁感应强度B在时间△t内均匀减小至零,则此过程( )
如图所示,有一半径为r的导电圆环处于磁感应强度为B的匀强磁场中,磁场方向垂直纸面向里且与圆环平面垂直,圆环的电阻为R.若磁感应强度B在时间△t内均匀减小至零,则此过程( )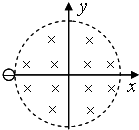 如图所示,有一半径为R、有明显边界的圆形匀强磁场区域,磁感应强度为B.今有一电子沿x轴正方向射入磁场,恰好沿y轴负方向射出.如果电子的荷质比为
如图所示,有一半径为R、有明显边界的圆形匀强磁场区域,磁感应强度为B.今有一电子沿x轴正方向射入磁场,恰好沿y轴负方向射出.如果电子的荷质比为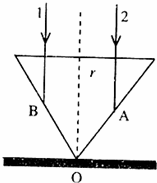 在桌面上有一个倒立的透明的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示.有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率为n=1.73.r为已知,求:
在桌面上有一个倒立的透明的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示.有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率为n=1.73.r为已知,求: