题目内容
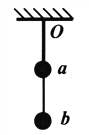
【题目】如图所示,光滑的轻滑轮通过支架固定在天花板上,一足够长的细绳跨过滑轮,一端悬挂小球b,另一端与套在水平细杆上的小球a连接。在水平拉力F作用下小球a从图示虚线(最初是竖直的)位置开始缓慢向右移动(细绳中张力大小视为不变)。已知小球b的质量是小球a的2倍,滑动摩擦力等于最大静摩擦力,小球a与细杆间的动摩擦因数为![]() 。则下列说法正确的是()
。则下列说法正确的是()

A. 当细绳与细杆的夹角为30°时,杆对a球的支持力为零
B. 支架对轻滑轮的作用力大小逐渐增加
C. 支架对a球的摩擦力先减小后增加
D. 若![]() 时,拉力F先减小后增加
时,拉力F先减小后增加
【答案】AC
【解析】设a的质量为m,则b的质量为2m;以b为研究对象,竖直方向受力平衡,可得绳子拉力始终等于b的重力,即T=2mg,保持不变;以a为研究对象,受力如图所示:
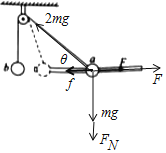
设绳子与水平方向夹角为![]() ,支持力
,支持力![]() ,向右缓慢拉动的过程中,
,向右缓慢拉动的过程中, ![]() 角逐渐减小,当
角逐渐减小,当![]() 时
时![]() ,解得
,解得![]() ,即
,即![]() ,故A正确;向右缓慢拉动的过程中,两个绳子之间的夹角逐渐增大,绳子的拉力不变,所以绳子的合力减小,则绳子对滑轮的作用力逐渐减小,故B错误;由图可知,角度
,故A正确;向右缓慢拉动的过程中,两个绳子之间的夹角逐渐增大,绳子的拉力不变,所以绳子的合力减小,则绳子对滑轮的作用力逐渐减小,故B错误;由图可知,角度![]() 从
从![]() 变到
变到![]() ,根据
,根据![]() ,可知,当角度
,可知,当角度![]() 从
从![]() 变到
变到![]() 时
时![]() 一直减小到零,当角度
一直减小到零,当角度![]() 从
从![]() 变到
变到![]() 时
时![]() 反向增大,故摩擦力先减小后增大,故C正确;由受力分析图,可知水平方向:
反向增大,故摩擦力先减小后增大,故C正确;由受力分析图,可知水平方向: ![]() ,由于
,由于![]() ,而
,而![]() ,若
,若![]() ,则
,则![]() ,故拉力为
,故拉力为![]() ,角度
,角度![]() 从
从![]() 变到
变到![]() 的过程中,当
的过程中,当![]() 时
时![]() 为最大,则拉力最大,当角度继续减小时,
为最大,则拉力最大,当角度继续减小时, ![]() 开始减小,则拉力也开始减小,故拉力F先增大后减小,故D错误;故选AC.
开始减小,则拉力也开始减小,故拉力F先增大后减小,故D错误;故选AC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目