题目内容
8.某同学设计了一个探究合力F不变时小车的加速度a与质量M关系的实验,图(a)所示为实验装置简图:(交流电的频率为50Hz)
(1)图(b)所示为某次实验得到的纸带,根据纸带可求出小车的加速度大小为0.51m/s2;(保留两位有效数字)
(2)保持砂和砂桶质量m不变,改变小车质量M,分别得到小车加速度a与质量M及对应$\frac{1}{M}$的数据.在如图(c)所示的坐标纸中画出了a-$\frac{1}{M}$图线,根据图线求出小车加速度a与质量倒数$\frac{1}{M}$之间的关系式是a=$\frac{1}{2M}$;
(3)若m=50g,改变M的值,进行多次实验,以下M的取值最不合适的一个是A.
A.M1=50gB.M2=500gC.M3=1kgD.M4=2kg.
分析 (1)纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的两个推论,可计算出打出某点时纸带运动的瞬时速度和加速度.
(2)根据表格中数据采用描点法画出图象,找出它们之间的关系;
(3)根据牛顿第二定律,运用整体法隔离法求出绳子拉力和砝码重力的关系,判断砝码重力等于滑行器合力的条件,从而确定正确的答案.
解答 解:(1)相邻计数点之间还有4个点未画出,说明相邻的计数点时间间隔为0.1s,
根据数据可知△x=6.70-6.19=7.21-6.70=7.72-7.21=0.51cm,
根据作差法得:
a=$\frac{△x}{{T}^{2}}$=$\frac{0.0051}{0.{1}^{2}}$=0.51m/s2;
(2)由图表分析可知在数值上物体加速度a的6倍等于物体质量的倒数即a=$\frac{1}{2}\frac{1}{M}$=$\frac{1}{2M}$.
(3)根据图表在坐标纸上描点,然后用一条直线将这些点和坐标原点连接起来,图象如图所示;
根据牛顿第二定律得,整体的加速度a=$\frac{mg}{M+m}$,隔离对滑行器分析,绳子的拉力F=Ma=$\frac{Mmg}{M+m}$=$\frac{mg}{1+\frac{m}{M}}$,
知到那个m远小于M时,砝码的重力等于滑行器的合力.所以最不合适的是:A;
故答案为:(1)0.51;(2)a=$\frac{1}{2M}$;(3)A.
点评 本题要求同学们能根据实验原理,运用作差法求出加速度,能根据表格分析加速度和小车质量之间的关系,分析出实验中存在问题的是本题的难点;
解决本题的关键知道砝码重力等于滑行器合力的条件,以及知道极短时间内的平均速度等于瞬时速度的大小.

练习册系列答案
相关题目
18.甲乙两船自身质量均为100kg,都静止在静水中,当一个质量为60kg的人从甲船跳上乙船后,不计水阻力,甲、乙两船速度大小之比v甲:v乙( )
| A. | 1:1 | B. | 8:5 | C. | 5:3 | D. | 10:3 |
16. 简谐横波在t=0时刻的波形图如图所示,abcd是介质中4个振动质点,此时a质点向平衡位置运动,波的波速大小为v=2m/s,由此可知( )
简谐横波在t=0时刻的波形图如图所示,abcd是介质中4个振动质点,此时a质点向平衡位置运动,波的波速大小为v=2m/s,由此可知( )
 简谐横波在t=0时刻的波形图如图所示,abcd是介质中4个振动质点,此时a质点向平衡位置运动,波的波速大小为v=2m/s,由此可知( )
简谐横波在t=0时刻的波形图如图所示,abcd是介质中4个振动质点,此时a质点向平衡位置运动,波的波速大小为v=2m/s,由此可知( )| A. | 该列波的频率是5Hz | |
| B. | 该列波沿x轴负向传播 | |
| C. | 从t=0时刻开始,经0.2s时间,4个质点所通过的路程均相等 | |
| D. | 在t=0.3s时刻,c的位移最大,d的位移为0 | |
| E. | 从t=0.4s时刻算起,质点a将比b先到达其平衡位置 |
13.下列说法中正确的是( )
| A. | 物体辐射电磁波的强度分布只与物体温度和辐射波的波长有关 | |
| B. | 对于同一种金属来说,其截止频率恒定,与入射光的频率及光的强度均无关 | |
| C. | 极少数α粒子的偏转角超过了90°,表明原子中带负电的物质体积很小 | |
| D. | 玻尔的能级原子模型虽然使用了定态、跃迁、量子等概念但保留“轨道”是其缺陷 | |
| E. | 光衍射现象中,产生明条纹的地方光子出现的概率低,这是波粒二象性的观点 | |
| F. | 做示踪原子的物质尽可能选用半衰期长一些的放射性元素 | |
| G. | 核力具有饱和性和短程性,原子核为了稳定,故重核在形成时其中子数多于质子数 | |
| H. | 比结合能小的原子核结合成或分解成比结合能大的原子核时一定释放核能 |
20. 如图,可视为质点的小木块放在静止在光滑水平面的长木板右端,木板和木块之间的接触面是粗糙的,当木板从静止开始受水平向右的恒定拉力作用而运动时,小木块相对于长木板向左滑动至左端,对此过程中下列判断正确的是( )
如图,可视为质点的小木块放在静止在光滑水平面的长木板右端,木板和木块之间的接触面是粗糙的,当木板从静止开始受水平向右的恒定拉力作用而运动时,小木块相对于长木板向左滑动至左端,对此过程中下列判断正确的是( )
 如图,可视为质点的小木块放在静止在光滑水平面的长木板右端,木板和木块之间的接触面是粗糙的,当木板从静止开始受水平向右的恒定拉力作用而运动时,小木块相对于长木板向左滑动至左端,对此过程中下列判断正确的是( )
如图,可视为质点的小木块放在静止在光滑水平面的长木板右端,木板和木块之间的接触面是粗糙的,当木板从静止开始受水平向右的恒定拉力作用而运动时,小木块相对于长木板向左滑动至左端,对此过程中下列判断正确的是( )| A. | 小木块相对于水平面做向右的加速运动 | |
| B. | 滑动摩擦力对木板做负功 | |
| C. | 拉力做功即合外力的功小于两物体动能增加的总和 | |
| D. | 两物体所组成的系统摩擦生热的量等于系统机械能的变化 |

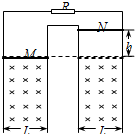 如图所示,竖直平面内有足够长、不计电阻的两组平行光滑金属导轨,宽度均为L=0.5m,上方连接一个阻值R=1Ω的定值电阻,虚线下方的区域内存在垂直纸面向里的磁感应强度B=2T的匀强磁场.完全相同的两根金属杆M和N靠在导轨上,金属杆的长度与导轨等宽且与导轨接触良好,两金属杆的电阻均为r=0.5Ω.将金属杆M固定在磁场的上边缘(仍在此磁场内),金属杆N从磁场边界上方h0=0.8m处由静止释放,进入磁场后恰好做匀速运动,g取10m/s2.求:
如图所示,竖直平面内有足够长、不计电阻的两组平行光滑金属导轨,宽度均为L=0.5m,上方连接一个阻值R=1Ω的定值电阻,虚线下方的区域内存在垂直纸面向里的磁感应强度B=2T的匀强磁场.完全相同的两根金属杆M和N靠在导轨上,金属杆的长度与导轨等宽且与导轨接触良好,两金属杆的电阻均为r=0.5Ω.将金属杆M固定在磁场的上边缘(仍在此磁场内),金属杆N从磁场边界上方h0=0.8m处由静止释放,进入磁场后恰好做匀速运动,g取10m/s2.求: 如图所示为一速度选择器,内有一磁感应强度为B,方向垂直纸面向外的匀强磁场,一个质子以速度v水平射人,为使粒子流经磁场时不偏转(不计重力),则磁场区域内必须同时存在一个匀强电场,此电场必须是:大小E=vB,方向竖直向上(填“向上”或“向下”)
如图所示为一速度选择器,内有一磁感应强度为B,方向垂直纸面向外的匀强磁场,一个质子以速度v水平射人,为使粒子流经磁场时不偏转(不计重力),则磁场区域内必须同时存在一个匀强电场,此电场必须是:大小E=vB,方向竖直向上(填“向上”或“向下”)