题目内容
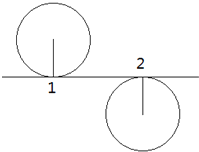
【题目】在十字路口,汽车以a=2m/s2的加速度从停车线启动做匀加速直线运动,此时有一辆自行车恰好通过停车线,与汽车同方向匀速行驶,行驶的速度大小V0=6m/s。求:
(1)经过多长时间汽车和自行车相距最远?最远距离是多少?
(2)在距停车线多远时汽车追上自行车?追到时汽车的速度是多大?
【答案】(1)3s,9m(2)36m;12m/s
【解析】
(1)汽车与自行车速度相同时,两者相距最远;根据速度时间关系列式求解时间,根据位移时间关系求解最远距离;(2)当两者位移相等时汽车追上自行车,列式即可求解.
(1)汽车与自行车速度相同时,两者相距最远;设所用时间为t,最远距离为xm,
则有v0=at 解得t=3s;
设相距最远时汽车的位移为x1,自行车的位移为x2,则
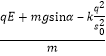
![]()
x2=v0t,
最大距离:xm=x2-x1
联立解得xm=9m
(2)设汽车经过时间t′在距停车线x处追上自行车,此时汽车的速度大小为v,则v=at′
![]()
x=v0t′
联立解得x=36m; v=12m/s
即汽车在距离停车线36m处追上自行车,此时汽车的速度为12m/s.

【题目】利用电流表和电压表测定一节干电池的电动势和内电阻.要求尽量减小实验误差.
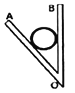
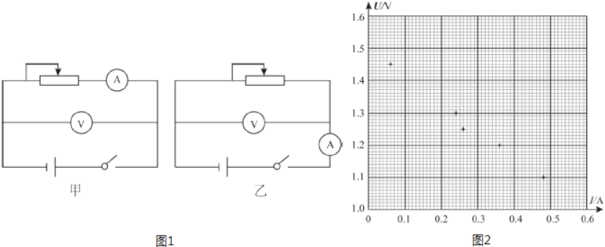
(1)应该选择的实验电路是图1中的_____(选项“甲”或“乙”).
(2)现有电流表(0﹣0.6A)、开关和导线若干,以及以下器材:
A.电压表(0﹣15V) B.电压表(0﹣3V)
C.滑动变阻器(0﹣50Ω) D.滑动变阻器(0﹣500Ω)
实验中电压表应选用_____;滑动变阻器应选用_____;(选填相应器材前的字母)
(3)某位同学记录的6组数据如下表所示,其中5组数据的对应点已经标在图2的坐标纸上,请标出余下一组数据的对应点,并画出U﹣I图线._____
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
电压U(V) | 1.45 | 1.40 | 1.30 | 1.25 | 1.20 | 1.10 |
电流I(A) | 0.060 | 0.120 | 0.240 | 0.260 | 0.360 | 0.480 |
(4)根据(3)中所画图线可得出干电池的电动势E=_____v,内电阻r=_____Ω
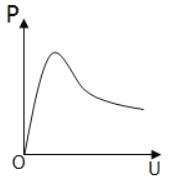
(5)实验中,随着滑动变阻器滑片的移动,电压表的示数U以及干电池的输出功率P都会发生变化.各示意图中正确反映P﹣U关系的是_____.
A、 B、
B、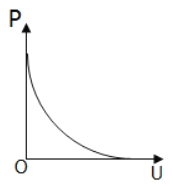
C、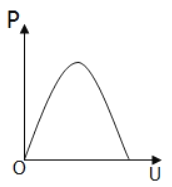 D、
D、