题目内容
如图所示，斜面和水平面由一小段光滑圆弧连接，斜面的倾角为37°，一质量为0.5kg的物块从斜面上距斜面底端B点5m处的A点由静止释放．已知物块与水平面和斜面的动摩擦因数均为0.3。（sin37°=0.6，cos37°=0.8，g=10m/s2）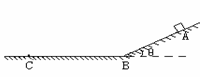
（1）物块在水平面上滑行的时间为多少？
（2）若物块开始静止在水平面上距B点10m 的C点处，用大小为4.5N的水平恒力向右拉该物块，到B点撤去此力，物块第一次到A点时的速度为多大？
（3）若物块开始静止在水平面上距B点10m 的C点处，用大小为4.5N的水平恒力向右拉该物块，欲使物块能到达A点，水平恒力作用的最短距离为多大？
（1）2s ；（2） 6m/s ；（3） 8m
解析试题分析: （1）物块先沿斜面匀加速下滑，设AB长度为L，动摩擦因数为μ，
下滑的加速度mgsinθ-μmgcosθ=ma
解得：a=gsinθ-μgcosθ=3.6m/s2；
到达B点时速度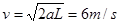
在水平面上物块做匀减速运动，则有：μmg=ma′
解得：a′=μg=3m/s2；
在水平面上运动的时间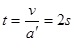
；
（2）设CB距离为，全过程用动能定理，
则有：（F-μmg）-mgLsin37°-μmgLcos37°=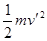
解得：v′=6m/s；
（3）设力作用的最短距离为′，
根据动能定理可得：F′-μmg-mgLsin37°-μmgLcos37°=0
解得：′=8m，
考点：动能定理；牛顿第二定律
练习册系列答案
相关题目
，求：
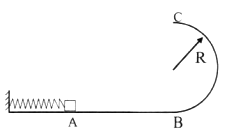
。质量为2.0kg的金属杆ab垂直导轨放置，其他电阻不计。用恒力沿导轨平面向下拉金属杆ab，由静止开始运动，8s末杆运动刚好达到最大速度为8m/s，这8s内金属杆的位移为48m，(g=10m/s2,cos370=0.8,sin370=0.6)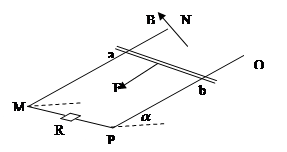
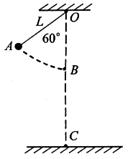
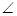AOB=37o，圆弧的半径R=0．5m；BD部分水平，长度为0．2m，C为BD的中点。现有一质量m=lkg，可视为质点的物块从A端由静止释放，恰好能运动到D点。（g=10m/s2，sin37o=0．6，cos37o=0．8）求：
，
