题目内容
某兴趣小组设计了如图所示的玩具轨道,它由细圆管弯成,固定在竖直平面内。左右两侧的斜直管道PA与PB的倾角、高度、粗糙程度完全相同,管口A、B两处均用很小的光滑小圆弧管连接(管口处切线竖直),管口到底端的高度H1=0.4m。中间“8”字型光滑细管道的圆半径R=10cm(圆半径比细管的内径大得多),并与两斜直管道的底端平滑连接。一质量m=0.5kg的小滑块从管口 A的正上方H2处自由下落,第一次到达最低点P的速度大小为10m/s.此后小滑块经“8”字型和PB管道运动到B处竖直向上飞出,然后又再次落回,如此反复。小滑块视为质点,忽略小滑块进入管口时因碰撞造成的能量损失,不计空气阻力,且取g=10m/s2。求:
(1) 滑块第一次由A滑到P的过程中,克服摩擦力做功;
(2)滑块第一次到达“8”字型管道顶端时对管道的作用力;
(3)滑块第一次离开管口B后上升的高度;
(4)滑块能冲出槽口的次数。
(1)2J;(2)455N,方向向上;(3)4.2m;(4)6次;
解析试题分析:(1)滑块第一次由A滑到P的过程中,克服摩擦力做功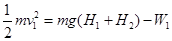 ,代入数据可得:W1=2J
,代入数据可得:W1=2J
(2)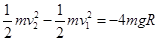 ,在“8”字型管道最高点
,在“8”字型管道最高点 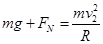
管道对滑块的弹力大小FN=455N,方向向下;滑块对管道的弹力大小FN/=455N,方向向上;
(3)滑块对此由A到B克服摩擦阻力做的功W2=2W1=4J;
Mg(H2-h)=W2
上升的高度h=4.2m
(4)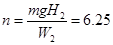 ,所以滑块能离开管口的次数为6次。
,所以滑块能离开管口的次数为6次。
考点:能量守恒定律及牛顿第二定律。

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
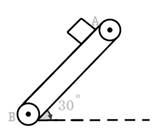
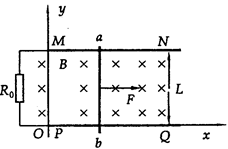
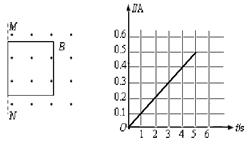
 =7m/s的初速从左侧磁场边缘水平进入磁场,求:
=7m/s的初速从左侧磁场边缘水平进入磁场,求:
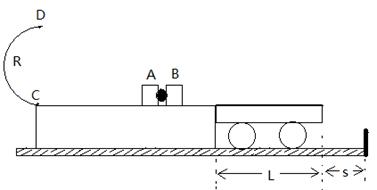

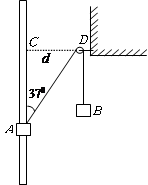
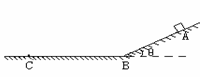
 ,物块A恰能保持静止.现在物块B的下端再挂一个小物块Q,物块A可从图示位置上升并恰好能到达C处.不计摩擦和空气阻力,
,物块A恰能保持静止.现在物块B的下端再挂一个小物块Q,物块A可从图示位置上升并恰好能到达C处.不计摩擦和空气阻力, 、
、 ,重力加速度g取10m/s2.求:
,重力加速度g取10m/s2.求: