题目内容
质量m=0.6kg的篮球从距地板H=0.80m高处由静止释放，与水平地板撞击后反弹上升的最大高度h=0.45m．从释放到弹跳至h高处经历的时间t=1.1s，忽略空气阻力，取g=10m/s2．求：（1）篮球与地板撞击过程中损失的机械能．
（2）地板对篮球的平均作用力．
【答案】分析：（1）篮球与地板撞击过程中损失的机械能等于初始时刻机械能减去末时刻机械能，初末位置物体动能为零，只有势能；
（2）分别根据自由落体运动求出篮球与地面碰撞前后的速度，再求出下落和上升的时间，根据总时间求出球与地面接触的时间，根据动量定律即可求解．
解答：解：（1）篮球与地板撞击过程中损失的机械能为：△E=mgH-mgh=0.6×10×（0.8-0.45）J=2.1J
（2）设篮球从H高处下落到地板所用时间为t1，刚接触地板时的速度为v1；反弹离地时的速度为v2，上升的时间为t2，由动能定理和运动学公式
下落过程：mgH=
，解得：v1=4m/s，
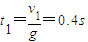
上升过程：-mgh=0-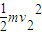
，解得：v2=3m/s，
篮球与地板接触时间为△t=t-t1-t2=0.4s
设地板对篮球的平均撞击力为F，由动量定理得：
（F-mg）△t=mv2+mv1
解得：F=16.5N
根据牛顿第三定律，篮球对地板的平均撞击力 F′=F=16.5N，方向向下
答：（1）篮球与地板撞击过程中损失的机械能为2.1J．
（2）地板对篮球的平均作用力为16.5N，方向向下．
点评：本题主要考查了自由落体运动的基本规律，在与地面接触的过程中，合外力对物体的冲量等于物体动量的变化量，难度适中．
（2）分别根据自由落体运动求出篮球与地面碰撞前后的速度，再求出下落和上升的时间，根据总时间求出球与地面接触的时间，根据动量定律即可求解．
解答：解：（1）篮球与地板撞击过程中损失的机械能为：△E=mgH-mgh=0.6×10×（0.8-0.45）J=2.1J
（2）设篮球从H高处下落到地板所用时间为t1，刚接触地板时的速度为v1；反弹离地时的速度为v2，上升的时间为t2，由动能定理和运动学公式
下落过程：mgH=
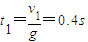
，解得：v1=4m/s，上升过程：-mgh=0-
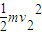，解得：v2=3m/s，篮球与地板接触时间为△t=t-t1-t2=0.4s
设地板对篮球的平均撞击力为F，由动量定理得：
（F-mg）△t=mv2+mv1
解得：F=16.5N
根据牛顿第三定律，篮球对地板的平均撞击力 F′=F=16.5N，方向向下
答：（1）篮球与地板撞击过程中损失的机械能为2.1J．
（2）地板对篮球的平均作用力为16.5N，方向向下．
点评：本题主要考查了自由落体运动的基本规律，在与地面接触的过程中，合外力对物体的冲量等于物体动量的变化量，难度适中．
练习册系列答案
相关题目
如图所示，在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=2m的薄平板AB．平板的下端B与斜面底端C的距离为5m．在平板的上端A处放一质量m=0.6kg的滑块，滑块与平板间的动摩擦因数μ1=0.25，滑块可看作质点，开始时使平板和滑块都静止，之后将它们无初速释放．设平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.5，求滑块与平板下端B到达斜面底端C的时间差△t．（sin37°=0.60，cos37°=0.80，g取10m/s2）
如图所示，某人用轻绳牵住一只质量m=0.6kg的氢气球，因受水平风力的作用，系氢气球的轻绳与水平方向成37°角．已知空气对气球的浮力为15N，人的质量M=50kg，且人受的浮力忽略不计（sin37°=0.6，cos37°=0.8）．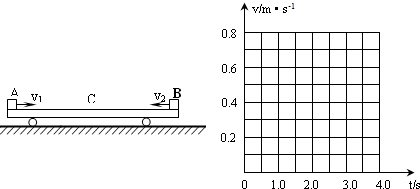
质量M=0.6kg的平板小车静止在光滑水面上，如图所示，当t=0时，两个质量都为m=0.2kg的小物体A和B，分别从小车的左端和右端以水平速度v1=5.0m/s和v2=2.0m/s同时冲上小车，当它们相对于小车停止滑动时，没有相碰．已知A、B两物体与车面的动摩擦因数都是0.20，取g=10m/s2，求：
如图所示，细绳一端系着质量M=0.6kg的物体，静止在水平平板上，另一端通过光滑小孔吊着质量m=0.3kg的物体，M的中点与圆孔距离为0.2m，并知M和水平面的最大静摩擦力为2N，现使此平板绕中心轴线转动，为保持物体与平板处于相对静止状态，问：