题目内容
3. 如图所示,有3块水平放置的长薄金属板a、b和c,a、b之间相距为L.紧贴b板下表面竖直放置半径为R的半圆形塑料细管,两管口正好位于小孔M、N处.板a与b、b与c之间接有电压可调的直流电源,板b与c间还存在方向垂直纸面向外的匀强磁场.调节板间电压Uba和Ubc,当Uba=U1、Ubc=U2时,质量为m、电荷量为q的带负电油滴,以速率v0从a板上的小孔竖直向下射入,油滴穿过b板M孔进入细管,恰能与细管无接触地从N孔射出.忽略小孔和细管对电场的影响,不计空气阻力.求:
如图所示,有3块水平放置的长薄金属板a、b和c,a、b之间相距为L.紧贴b板下表面竖直放置半径为R的半圆形塑料细管,两管口正好位于小孔M、N处.板a与b、b与c之间接有电压可调的直流电源,板b与c间还存在方向垂直纸面向外的匀强磁场.调节板间电压Uba和Ubc,当Uba=U1、Ubc=U2时,质量为m、电荷量为q的带负电油滴,以速率v0从a板上的小孔竖直向下射入,油滴穿过b板M孔进入细管,恰能与细管无接触地从N孔射出.忽略小孔和细管对电场的影响,不计空气阻力.求:(1)油滴进入M孔时的速度v1;
(2)b、c两板间的电场强度E和磁感应强度B的值;
(3)当油滴从细管的N孔射出瞬间,将Uba和B立即调整到U1′和B′,使油滴恰好不碰到a板,且沿原路与细管无接触地返回并穿过M孔,求U1′和B′.
分析 (1)油滴开始下落的过程中有重力、电场力做功,根据动能定理求出油滴进入M孔的速度.
(2)油滴进入电场、磁场共存区域,恰与细管无接触地从N孔射出,知电场力等于重力,洛伦兹力提供向心力,根据平衡求出电场强度的大小,根据洛伦兹力提供向心力求出磁感应强度的大小.
(3)若油滴恰不能撞到a板,且再返回并穿过M点速度为零,根据动能定理求出U′ab的大小,返回到N孔时速度大小不变,现向左偏转做匀速圆周运动,则磁感应强度的大小不变,方向改变.
解答 解:(1)油滴入电场后,重力与电场力均做功,设到M点时的速度为v1,由动能定理$\frac{1}{2}mv_1^2-\frac{1}{2}mv_0^2=mgL+q{U_1}$①
得:${v}_{1}=\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{m}}$ ②
(2)油滴进入电场、磁场共存区域,恰与细管无接触地从N孔射出,须电场力与重力平衡,有:mg=qE ③
得:$E=\frac{mg}{q}$ ④
油滴在半圆形细管中运动时,洛伦兹力提供向心力,$q{v}_{1}B=\frac{m{v}_{1}^{2}}{R}$ ⑤
得$B=\frac{m{v}_{1}}{qR}=\frac{m}{qR}\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{m}}$ ⑥
(3)若油滴恰不能撞到a板,且再返回并穿过M点,由动能定理,$0-\frac{1}{2}mv_1^2=-mgL-qU'_{ba}^{\;}$⑧
得:$U{′}_{ba}^{\;}={U}_{1}+\frac{m{v}_{0}^{2}}{2q}$⑨
考虑到油滴返回时速度方向已经相反,为了使油滴沿原路与细管无接触地返回并穿过M孔,磁感应强度的大小不变,方向相反,即:
B?=-B⑩
答:(1)油滴进入M孔时的速度$\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{m}}$.
(2)b、c两板间的电场强度$\frac{mg}{q}$,磁感应强度$\frac{m}{qR}\sqrt{{v}_{0}^{2}+2gL+\frac{2q{U}_{1}}{m}}$.
(3)U1′和B′分别为:${U}_{1}+\frac{m{v}_{0}^{2}}{2q}$,B?=-B.
点评 本题考查带电粒子在复合场中的运动,关键理清粒子的运动情况,结合牛顿第二定律和动能定理进行求解.

 名校课堂系列答案
名校课堂系列答案 如图所示,A、B和O位于同一条直线上,波源O产生的横波沿该直线向左右两侧传播,波速均为5m/s.当波源起振后经过时间6s,A点起振,又经过时间4s,B点起振,此后A、B两点的振动方向始终相反,则下列说法中正确的是( )
如图所示,A、B和O位于同一条直线上,波源O产生的横波沿该直线向左右两侧传播,波速均为5m/s.当波源起振后经过时间6s,A点起振,又经过时间4s,B点起振,此后A、B两点的振动方向始终相反,则下列说法中正确的是( )| A. | A、B两点的起振方向相反 | |
| B. | A、B两点之间的距离一定为半波长的奇数倍 | |
| C. | 这列横波的波长可能为4m | |
| D. | 波源振动周期可能为1.6s |
| A. | 飞船受到的万有引力逐渐增大,线速度逐渐减小 | |
| B. | 飞船的向心加速度逐渐增大,周期逐渐减小,线速度和角速度都逐渐增大 | |
| C. | 飞船的动能、重力势能和机械能都逐渐减小 | |
| D. | 重力势能逐渐减小,动能逐渐增大,机械能逐渐减小 |
| A. | 在用单摆测定重力加速度的实验中,必须从最大位移处开始计时 | |
| B. | 光速不变原理是:真空中的光速在不同的惯性参考系中都是相同的 | |
| C. | 两列波叠加产生干涉现象,振动加强区域与减弱区域应交替变化 | |
| D. | 光的偏振现象说明光波是横波 | |
| E. | 用绿光做双缝干涉实验,在光屏上呈现出明暗相间的条纹,相邻两条绿条纹间的距离为△X,如果只增大双缝到光屏之间的距离,△X将减小 |
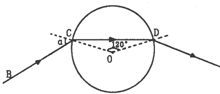 如图所示,真空中有一半径为R、圆心为O的均匀玻璃球,频率一定的细激光束在真空中沿BC传播,从C点经折射进入玻璃球,并经出射点D折射出去,已知∠COD=120°,玻璃对该激光的折射率为$\sqrt{3}$,则下列说法中正确的是( )
如图所示,真空中有一半径为R、圆心为O的均匀玻璃球,频率一定的细激光束在真空中沿BC传播,从C点经折射进入玻璃球,并经出射点D折射出去,已知∠COD=120°,玻璃对该激光的折射率为$\sqrt{3}$,则下列说法中正确的是( )| A. | 激光束在C点的入射角α=60° | |
| B. | 此激光束在玻璃中穿越的时间为t=$\frac{3R}{c}$ | |
| C. | 一个光子在穿过玻璃球的过程中能量逐渐变小 | |
| D. | 改变入射角α的大小,细激光束可能在球表面D处发生全反射 |
 如图,匝数为100匝的矩形线圈abcd处于磁感应强度B=$\frac{6\sqrt{2}}{25π}$T的水平匀强磁场中,线圈面积S=0.5m2,内阻不计.线圈绕垂直于磁场的轴以角速度ω=10πrad/s匀速转动.线圈通过金属滑环与理想变压器原线圈相连,变压器的副线圈接入一只“12V,12W”灯泡,灯泡正常发光,下列说法中正确的是( )
如图,匝数为100匝的矩形线圈abcd处于磁感应强度B=$\frac{6\sqrt{2}}{25π}$T的水平匀强磁场中,线圈面积S=0.5m2,内阻不计.线圈绕垂直于磁场的轴以角速度ω=10πrad/s匀速转动.线圈通过金属滑环与理想变压器原线圈相连,变压器的副线圈接入一只“12V,12W”灯泡,灯泡正常发光,下列说法中正确的是( )| A. | 通过灯泡的交变电流的频率是50Hz | |
| B. | 矩形线圈中产生的电动势的最大值为120V | |
| C. | 变压器原、副线圈匝数之比为10:1 | |
| D. | 若将灯泡更换为“12V,24W”且保证其正常发光,需要增大矩形线圈的转速 |
| A. | 温度相同的氢气和氮气,氢气分子比氨气分子的平均速率大 | |
| B. | 由阿伏加德罗常数、气体的摩尔质量和气体的密度,可以估算出理想气体分子间的平均距离 | |
| C. | 当理想气体的体积增加时,气体的内能一定增大 | |
| D. | 将碳素墨水滴入清水中,观察到布朗运动是碳分子的无规则运动 | |
| E. | 容器内一定质量的理想气体体积不变,温度升高,则单位时间内撞击容器壁的分子数增加 |
 某直角三棱镜截面如图所示,已知∠A=30°,BC边长为2$\sqrt{3}$L,材料折射率n=$\sqrt{3}$.一个较大的光屏MN平行于BC边竖直放置,且与BC边间距为2L.一平行单色光平行AC射到AB面上,则( )
某直角三棱镜截面如图所示,已知∠A=30°,BC边长为2$\sqrt{3}$L,材料折射率n=$\sqrt{3}$.一个较大的光屏MN平行于BC边竖直放置,且与BC边间距为2L.一平行单色光平行AC射到AB面上,则( )| A. | 一定有光线从AC边射出 | |
| B. | 屏上、下两部分被照亮,中间存在未照亮的阴影,屏向左移动L刚好消除中间阴影 | |
| C. | 屏上、下两部分被照亮,中间存在未照亮的阴影,屏向右移动L刚好消除中间阴影 | |
| D. | 屏上被照亮部分的竖直总长度为4$\sqrt{3}$L |
 一列频率为2.5Hz的简谐横波沿x轴传播,在t1=0时刻波形如图中实线所示,在t2=0.7s时刻波形如图中虚线所示.则该波沿x轴负向(填“正向”或“负向”)传播.其传播速度为10m/s.在t3=0.9s时位于0<x<4m区间的部分质点正在向y轴正方向运动,这些质点在x轴上的坐标区间是1m<x<3m.
一列频率为2.5Hz的简谐横波沿x轴传播,在t1=0时刻波形如图中实线所示,在t2=0.7s时刻波形如图中虚线所示.则该波沿x轴负向(填“正向”或“负向”)传播.其传播速度为10m/s.在t3=0.9s时位于0<x<4m区间的部分质点正在向y轴正方向运动,这些质点在x轴上的坐标区间是1m<x<3m.