题目内容
【题目】如图所示,物体A、B叠放在倾角θ=37°的斜面上(斜面保持不动,质量为M=10 kg),并通过跨过光滑滑轮的细线相连,细线与斜面平行.两物体的质量分别mA=2 kg,mB=1 kg, B与斜面间的动摩擦因数μ2=0.2,问:(认为滑动摩擦力等于最大静摩擦力,g取10 m/s2,sin 37°=0.6)
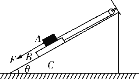
(1)如果A、B间动摩擦因数μ1=0.1,为使A能平行于斜面向下做匀速运动,应对A施加一平行于斜面向下的多大F的拉力?此时斜面对地面的压力N多大?
(2)如果A、B间摩擦因数不知,为使AB两个物体一起静止在斜面上,AB间的摩擦因数μ1应满足什么条件.
【答案】(1)F=2 N ; N=131.2 N (2) ![]() 0.0375
0.0375
【解析】
(1)对A: F+mAgsin θ=T+μ1mAgcos θ
对B:T=mBgsin θ+μ1mAgcos θ+μ2(mA+mB)gcos θ
可解得:F=2 N
利用整体法:N=(M+mA+mB)g+Fsin θ=131.2 N
(2)由受力分析可知,一定存在A有下滑趋势,B有上滑趋势.
对A:mAgsin θ=μ1mAgcos θ+T
对B:T=μ1mAgcos θ+μ2(mA+mB)gcos θ+mBgsin θ
解得最小值:μ1min=![]() =0.0375
=0.0375
则:μ1≥0.0375

练习册系列答案
相关题目