题目内容
【题目】如图所示,水平地面上固定一半径为R=0.8m的![]() 光滑圆弧轨道,轨道左端放一质量为M=3kg、长为L=l.75m的木板,木板上表面与轨道末端等高,木板与地面间无摩擦,其左端放一质量m=lkg的物块,物块与木板间的动摩擦因数为=0.4。现给物块施一水平向右的恒力F=15N,作用一段距离x后撤去F,物块正好能滑到圆弧轨道的最高点,然后再滑回,取g=l0m/s2。
光滑圆弧轨道,轨道左端放一质量为M=3kg、长为L=l.75m的木板,木板上表面与轨道末端等高,木板与地面间无摩擦,其左端放一质量m=lkg的物块,物块与木板间的动摩擦因数为=0.4。现给物块施一水平向右的恒力F=15N,作用一段距离x后撤去F,物块正好能滑到圆弧轨道的最高点,然后再滑回,取g=l0m/s2。
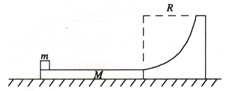
(1)求物块滑到板右端时的速度v多大;
(2)求x的大小;
(3)通过计算说明,物块最终能否滑离木板。
【答案】(1) 4m/s (2) lm (3) 物块不会滑离木板
【解析】(1)对于物块从轨道底端上升到顶端的过程,由机械能守恒可得:![]()
解得:v=4m/s
(2)对于物块从木板左端滑到右端的过程,由动能定理可得: ![]()
解得:x=lm
(3)设物块相对板向左滑动距离x后,与木板达到相同速度![]() ,由动量守恒定律得:
,由动量守恒定律得:![]()
解得:![]()
由能量守恒定律得:![]()
解得:x=1.5m<L=1.75m
故物块不会滑离木板

练习册系列答案
相关题目