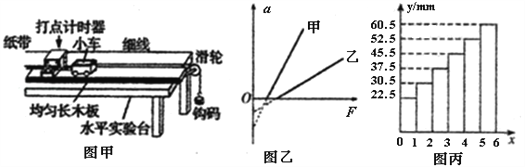
��Ŀ����
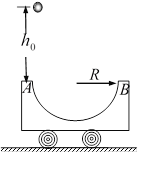
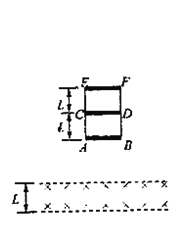
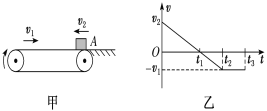
����Ŀ����ͼ��ʾ����Եˮƽ���������![]() ��������A��B������A������Ϊ2m�������Ϊ+q��B������Ϊm�IJ�����Ľ������顣�ռ������ˮƽ�������ǿ�糡����ǿΪ
��������A��B������A������Ϊ2m�������Ϊ+q��B������Ϊm�IJ�����Ľ������顣�ռ������ˮƽ�������ǿ�糡����ǿΪ![]() ����֪A��ˮƽ���Ķ�Ħ������
����֪A��ˮƽ���Ķ�Ħ������![]() ��B��ˮƽ���Ķ�Ħ������
��B��ˮƽ���Ķ�Ħ������![]() ��A��B����ײΪ������������ײʱ�伫�̣���ײ��A��B�����������ͬ���ܵ����ʼ�ղ��䣨gȡ10m/s2��������
��A��B����ײΪ������������ײʱ�伫�̣���ײ��A��B�����������ͬ���ܵ����ʼ�ղ��䣨gȡ10m/s2��������
��1��A��һ����B��ǰ���ٶ�![]() �Ĵ�С��
�Ĵ�С��
��2��A�ڶ�����B��ǰ���ٶȴ�С��
��3��A��Bֹͣ�˶�ʱ��B����λ��![]() ��
��
���𰸡���1��2m/s����2��![]() ����3��
����3��![]()
��������
��1����A��ʼ�˶�����B��ײ����,�ɶ��ܶ����ã�
![]() ��
��
�������ݽ�ã�
v0=2m/s��
��2��AB��ײ����ϵͳ�����غ㣬�ɶ����غ㶨�ɵã�
2mv0=2mv1+mv2��
�ɻ�е���غ㶨�ɵã�
![]() ��
��
�������ݽ�ã�
![]() ��
��![]() ��
��
��������ײ��������֣���Ϊ![]() ����B�ļ��ٶȣ�
����B�ļ��ٶȣ�
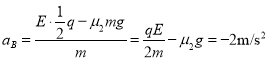 ��
��
A�ļ��ٶȣ�
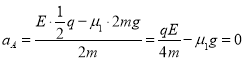 ��
��
��B���ȼ����˶���A�������˶���
A�ڶ�����B��ǰ���ٶȴ�СΪ��
![]() ��
��
��3��B�������˶�ֱ��ֹͣ��λ�ƣ�
![]() ��
��
AB�ڶ�����ײ����ϵͳ�����غ㡢��е���غ㣬
�ɶ����غ㶨�ɵã�
2mv1=2mv��1+mv��2��
�ɻ�е���غ㶨�ɵã�
![]() ��
��
�������ݽ�ã�
![]() ��
��
![]() ��
��
B�ٴ�ֹͣʱ��λ��
![]() ��
��
��A.Bֹͣ�˶�ʱ��B����λ�ƣ�x=x1+x2=![]() ��
��

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�