题目内容
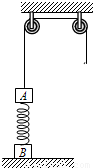
如图所示,质量为m1的物体A 经一轻质弹簧与下方地面上质量为m2的物体B相连,弹簧的劲度系数为k,A、B 都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩,不计绳与滑轮间的摩擦,开始时各段绳都处于伸直状态,A上方的一段绳沿竖直方向,重力加速度为g.(1)求弹簧的压缩量;
(2)现施加一恒力F竖直向下拉挂钩,求物块B刚要离开地面时物块A的加速度;
(3)在(2)中,若物块B刚要离开地面时,物块A的速度为v,求从开始施加拉力F到物块B刚要离开地面过程中,弹簧弹力对物块A所做的功;
(4)若在挂钩上挂一质量为m3的物体C 并从静止开始释放,恰好能使物块B离开地面,求此过程中弹簧弹力对物块A所做的功.
【答案】分析:(1)根据胡克定律即可求解;
(2)B刚要离开地面时,B受弹簧弹力F2和重力作用处于静止状态,求出弹力,对A进行受力分析,根据牛顿第二定律即可求解;
(3)先求出B刚要离开地面时,弹簧的伸长量,此过程中以A为研究对象,根据动能定理列式即可求解;
(4)分析题意可知,B不再上升,表明此时A和C的速度为零,C已降到最低点.以A、C和弹簧为研究对象,根据机械能守恒定律,求出弹簧弹性势能增加量
即可求解.
解答:解:(1)根据胡克定律F1=kx1 得x1=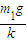
(2)B刚要离开地面时,B受弹簧弹力F2和重力作用处于静止状态,则
F2=m2g
F-F2-m1g=m1a
a=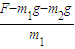
(3)B刚要离开地面时,弹簧的伸长量为x2
kx2=m2g
此过程中以A为研究对象,根据动能定理
WF+WG+W弹= m1v2-0
m1v2-0
重力和拉力做功分别为
WG=-m1g(x1+x2)
WF=F(x1+x2 )
得W弹= m1v2+(m1g-F)
m1v2+(m1g-F)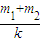 g
g
(4)分析题意可知,B不再上升,表明此时A和C的速度为零,C已降到最低点.
以A、C和弹簧为研究对象,根据机械能守恒定律,弹簧弹性势能增加量为
△Ep=m3g(x1+x2)-m1g(x1+x2)
得△Ep=( m3g-m1g)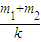 g
g
弹力对A所做的功W=-△Ep=(m1g-m3g)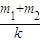 g
g
答:(1)弹簧的压缩量为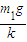 ;
;
(2)物块B刚要离开地面时物块A的加速度为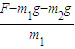 ;
;
(3)在(2)中,若物块B刚要离开地面时,物块A的速度为v,从开始施加拉力F到物块B刚要离开地面过程中,
弹簧弹力对物块A所做的功为 m1v2+(m1g-F)
m1v2+(m1g-F)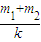 g;
g;
(4)若在挂钩上挂一质量为m3的物体C 并从静止开始释放,恰好能使物块B离开地面,此过程中弹簧弹力对物块A所做的功为(m1g-m3g)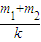 g.
g.
点评:本题关键分析清楚物体的运动规律,然后根据平衡条件和机械能守恒定律以及胡克定律列式后联立求解即可.
(2)B刚要离开地面时,B受弹簧弹力F2和重力作用处于静止状态,求出弹力,对A进行受力分析,根据牛顿第二定律即可求解;
(3)先求出B刚要离开地面时,弹簧的伸长量,此过程中以A为研究对象,根据动能定理列式即可求解;
(4)分析题意可知,B不再上升,表明此时A和C的速度为零,C已降到最低点.以A、C和弹簧为研究对象,根据机械能守恒定律,求出弹簧弹性势能增加量
即可求解.
解答:解:(1)根据胡克定律F1=kx1 得x1=
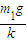
(2)B刚要离开地面时,B受弹簧弹力F2和重力作用处于静止状态,则
F2=m2g
F-F2-m1g=m1a
a=
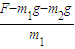
(3)B刚要离开地面时,弹簧的伸长量为x2
kx2=m2g
此过程中以A为研究对象,根据动能定理
WF+WG+W弹=
 m1v2-0
m1v2-0 重力和拉力做功分别为
WG=-m1g(x1+x2)
WF=F(x1+x2 )
得W弹=
 m1v2+(m1g-F)
m1v2+(m1g-F)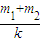 g
g (4)分析题意可知,B不再上升,表明此时A和C的速度为零,C已降到最低点.
以A、C和弹簧为研究对象,根据机械能守恒定律,弹簧弹性势能增加量为
△Ep=m3g(x1+x2)-m1g(x1+x2)
得△Ep=( m3g-m1g)
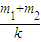 g
g弹力对A所做的功W=-△Ep=(m1g-m3g)
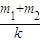 g
g 答:(1)弹簧的压缩量为
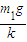 ;
;(2)物块B刚要离开地面时物块A的加速度为
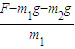 ;
;(3)在(2)中,若物块B刚要离开地面时,物块A的速度为v,从开始施加拉力F到物块B刚要离开地面过程中,
弹簧弹力对物块A所做的功为
 m1v2+(m1g-F)
m1v2+(m1g-F)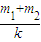 g;
g;(4)若在挂钩上挂一质量为m3的物体C 并从静止开始释放,恰好能使物块B离开地面,此过程中弹簧弹力对物块A所做的功为(m1g-m3g)
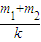 g.
g.点评:本题关键分析清楚物体的运动规律,然后根据平衡条件和机械能守恒定律以及胡克定律列式后联立求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,质量为m1=2.0kg、长为L=10.0m的平板小车,静止在光滑水平地面上,一质量为m2=0.5kg的小物块以v0=10.0m/s速度从左端冲上平板车,已知小物块与平板车之间的动摩擦因数μ=0.30.有关平板车和小物块最后的速度v'1和v'2的大小,以及整个过程中系统内能的增加量Q的计算试,正确的是(g=10m/s2)( )
如图所示,质量为m1=2.0kg、长为L=10.0m的平板小车,静止在光滑水平地面上,一质量为m2=0.5kg的小物块以v0=10.0m/s速度从左端冲上平板车,已知小物块与平板车之间的动摩擦因数μ=0.30.有关平板车和小物块最后的速度v'1和v'2的大小,以及整个过程中系统内能的增加量Q的计算试,正确的是(g=10m/s2)( )A、v′1=v′2=
| ||||||
B、v′1=v′2=
| ||||||
C、v′1<
| ||||||
D、v′1<
|
 如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(已知:sin37°=0.6,cos37°=0.8)求:
如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙均处于静止状态.(已知:sin37°=0.6,cos37°=0.8)求: 如图所示,质量为m1=10g的子弹以800m/s的速度向右射向放在光滑地面上静止的质量为2kg的物块.
如图所示,质量为m1=10g的子弹以800m/s的速度向右射向放在光滑地面上静止的质量为2kg的物块. (2011?河南模拟)如图所示,质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行,长木板保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与水平地面间的动摩擦因数为μ2,则( )
(2011?河南模拟)如图所示,质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行,长木板保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与水平地面间的动摩擦因数为μ2,则( ) (2009?崇文区一模)如图所示,质量为m1=1kg的小物块P置于桌面上的A点并与弹簧的右端接触(不拴接),轻弹簧左端固定,且处于原长状态.质量M=3.5kg、长L=1.2m的小车静置于光滑水平面上,其上表面与水平桌面相平,且紧靠桌子右端.小车左端放有一质量m2=0.5kg的小滑块Q.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,撤去推力,此后P沿桌面滑到桌子边缘C时速度为2m/s,并与小车左端的滑块Q相碰,最后Q停在小车的右端,物块P停在小车上距左端0.5m处.已知AB间距离L1=5cm,AC间距离L2=90cm,P与桌面间动摩擦因数μ1=0.4,P、Q与小车表面间的动摩擦因数μ2=0.1,(g取10m/s2),求:
(2009?崇文区一模)如图所示,质量为m1=1kg的小物块P置于桌面上的A点并与弹簧的右端接触(不拴接),轻弹簧左端固定,且处于原长状态.质量M=3.5kg、长L=1.2m的小车静置于光滑水平面上,其上表面与水平桌面相平,且紧靠桌子右端.小车左端放有一质量m2=0.5kg的小滑块Q.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,撤去推力,此后P沿桌面滑到桌子边缘C时速度为2m/s,并与小车左端的滑块Q相碰,最后Q停在小车的右端,物块P停在小车上距左端0.5m处.已知AB间距离L1=5cm,AC间距离L2=90cm,P与桌面间动摩擦因数μ1=0.4,P、Q与小车表面间的动摩擦因数μ2=0.1,(g取10m/s2),求: