题目内容
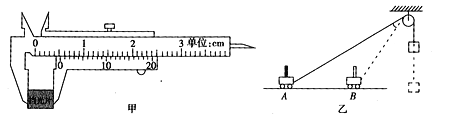
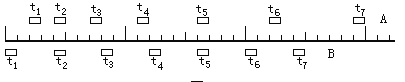
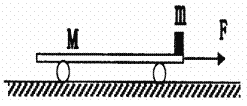
【题目】如图所示，质量为
的物块
（可看作质点），开始放在长木板
的左端， 
的质量为
，可在水平面上无摩擦滑动，两端各有一竖直挡板
、
，现
、
以相同的速度
向左运动并与挡板
发生碰撞．每次
只要与
碰后其速度立即变为
，但不与
粘接； 
与
碰后没有能量损失，碰后将接着返回向
板运动，且在每次与
板碰撞之前， 
、
均能达到共同速度并且立即被锁定，让其二者一起向
板运动，与
板碰撞后
、
一并原速反向，并且立即解除锁定． 
、
之间动摩擦因数
． 
取
．回答下列问题：
（
）在与
板发生第一次碰撞之前
， 
的共同速度是多少？ 
相对于
向右滑行距离
是多少．
（
）通过计算， 
与挡板
能否发生第二次碰撞．
（
）
和
最终停止在何处？ 
在
上一共通过了多少路程．
【答案】（
）
； 
．（
）
物块与
板能发生第二次碰撞．（
）停在
档板处， 
．
【解析】（
）设与
发生第一次碰前， 
、
共同运动速度为
， 
与
板第一次碰撞后的速度为
，根据题意得： 
．
对
、
在与
板碰后至
、
共同运动速度的过程中，由动量守恒定律得： 
代入数据计算得出： 
．
由能量守恒得： 
．
联立上式并代入数据计算得出： 
．
（
）
第二次与
板碰后，速度为零， 
物块在
板上做匀减速运动，设
物块能到达
板最左端，且到达最左端的速度为
，则由动能定理得： 
．
代入数据计算得出： 
．
因为
解合理，所以
物块与
板能发生第二次碰撞．
（3）第二次碰后
物块的速度仍为
，同理经过上述全过程到达
板最左端的速度为： 
，故
， 
能继续上述过程直至
速度减为
并停在
档板处．
同理得
物块在
板上滑行的距离： 
．
依此类推： 
．
．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
相关题目
