题目内容
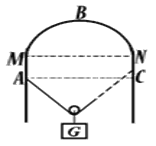
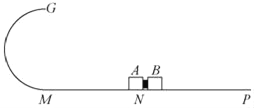
【题目】如图所示，左侧MG为光滑半圆形轨道，与水平光滑轨道平滑相连，半径为2m。水平轨道分为两段，MN为长L=1.5m的光滑水平轨道，NP部分粗糙且足够长，在水平轨道靠近N点处放着两个物块A、B，中间夹着炸药，储存了60J的化学能，某时刻引爆炸药。已知两物块与NP间的动摩擦因数μ=0.5，A、B质量分别为mA=3kg，mB=5kg。A、B可视为质点，假设化学能全部转化为机械能，且之后所有的碰撞为弹性碰撞。重力加速度g取10m/s2．关于A、B的运动，下列说法正确的是（ ）
A. 爆炸过程中，B受到的冲量大小为15Ns
B. 爆炸之后，A、B不会再次发生碰撞
C. 爆炸之后，A、B会发生碰撞，且碰后向同一方向运动
D. 最终A、B停止运动后的距离为1m
【答案】AD
【解析】
A、对爆炸过程，取向左为正方向，
由动量守恒定律得：mAvA﹣mBvB=0，
由能量守恒定律得：
J，
解得：vA=5m/s，vB=3m/s；
B受到的冲量为：IB=mBvB=5×3=15Ns，故A正确；
BC、爆炸结束后，假设A恰好能滑到与半圆轨道圆心等高处需要的速度为v0，
由机械能守恒定律得：mAgr= 
，解得：v0= 
m/s，
因为 vA＜v0，所以碰撞后A滑不到与半圆轨道圆心等高处，根据机械能守恒定律知，A返回N点时速度大小等于vA，因为vA＞vB，所以爆炸之后，A、B会发生碰撞，
碰撞时B已经静止，根据一动一静的完全弹性碰撞可得，A、B发生弹性碰撞，
因A质量小于B的质量，因此碰后A、B运动方向相反，故B错误，C错误；
D、对B，由动能定理得：μmBgxB=
，
从爆炸结束后到与B碰撞前，对A，由动能定理得：﹣μmAgxB=
，
A、B碰撞过程满足动量守恒、机械能守恒，
碰撞结束后，对A，由动能定理得：
，
对B，由动能定理得：
，
最终A、B间距：
，代入数据解得：d=1m，故D正确；
故选：AD。
