Question

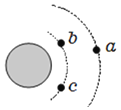
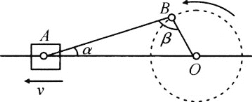
【题目】如图所示的机械装置可以将圆周运动转化为直线上的往复运动。连杆AB、OB可绕图中A、B、O三处的转轴转动，连杆OB在竖直面内的圆周运动可通过连杆AB使滑块在水平横杆上左右滑动。已知OB杆长为L，绕O点做逆时针方向匀速转动的角速度为ω，当连杆AB与水平方向夹角为α，AB杆与OB杆的夹角为β时，滑块的水平速度大小为( )

A. B. C. D.

Answer 1

【答案】D

【解析】

根据“连杆OB在竖直面内的圆周运动可通过连杆AB使滑块在水平横杆上左右滑动”、“滑块的水平速度大小为”可知，本题考查速度的合成与分解问题，根据两物体沿杆方向的速度相等，分别将A、B的速度沿杆和垂直杆分解，列式求解及可。

设滑块的水平速度大小为v，A点的速度的方向沿水平方向，如图将A点的速度分

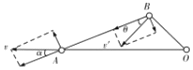
根据运动的合成与分解可知，沿杆方向的分速度：vA分=vcosα，

B点做圆周运动，实际速度是圆周运动的线速度，可以分解为沿杆方向的分速度和垂直于杆方向的分速度，如图设B的线速度为v′则：

vB分=v′cosθ=v′cos(90β)=v′sinβ， v′=ωL

又二者沿杆方向的分速度是相等的，即：vA分=vB分

联立可得：v=.故D正确，ABC错误

故选：D