题目内容
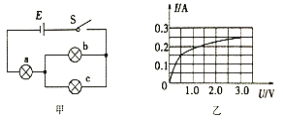
【题目】如图甲所示，轻绳一端固定在O点，另一端固定一小球(可看成质点)，让小球在竖直平面内做圆周运动。改变小球通过最高点时的速度大小v，测得相应的轻绳弹力大小F，得到F-v2图象如图乙所示，已知图线的延长线与纵轴交点坐标为(0，－b)，斜率为k。不计空气阻力，重力加速度为g，则下列说法正确的是
A. 该小球的质量为bg
B. 小球运动的轨道半径为
C. 图线与横轴的交点表示小球所受的合外力为零
D. 当v2=a时，小球的向心加速度为g
【答案】B
【解析】
利用受力，列牛顿第二定律公式，然后结合图像中的斜率和截距求解即可。
AB、小球在最高点时受到拉力为F，根据牛顿第二定律可知：
解得：
结合图像可知：
，即
，斜率
解得：
故A错；B对；
C、 图线与横轴的交点表示小球所受的拉力为零，即合外力等于重力时的情况，故C错；
D、根据向心加速度公式可知
，故D错；
故选B
练习册系列答案
相关题目
