题目内容
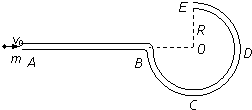
【题目】如图甲所示，在x轴上方存在随时间变化的匀强磁场（如图乙所示），磁感应强度大小为B，规定垂直于xOy平面向外为正方向；在x轴下方存在匀强电场，电场方向与xOy平面平行，且与x轴成30°夹角．在t=0时刻，一带正电的粒子以速度v0自y轴上P点沿y轴正方向射出，一段时间后进入电场，进入电场时的速度方向与电场方向相反．已知粒子的比荷 
= 
，磁场变化周期为T0 ， 忽略重力的影响．求：
（1）粒子自P点出发至第一次到达x轴时所需的时间；
（2）若使粒子能够回到P点，求电场强度的最大值．
【答案】
（1）
解：粒子在磁场中做匀速圆周运动洛伦兹力提供向心力，
由牛顿第二定律得：qv0B= 
…①
粒子做圆周运动的周期：T= 
…②
粒子自y轴上P点沿y轴正方向射出，进入电场时的速度方向与电场方向相反，粒子在磁场中转过的圆心角为：240°，
粒子在磁场中的运动时间：t= 
T …③
解得：t= 
（2）
解：粒子回到p点，粒子在电场中的运动时间应满足：
t=NT0 （N=1、2、3、） …④
在电场中，由牛顿第二定律得：
Eq=ma …⑤
由运动学规律得：
v0=a 
t …⑥
解得：E= 
，
当N=1时，电场强度最大为：Emax= 
= 
【解析】（1）粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律与粒子的周期公式求出粒子的运动时间．（2）分析清楚粒子在电场中的运动过程，应用牛顿第二定律、运动学公式求出电场强度的最大值．
【考点精析】解答此题的关键在于理解带电微粒（计重力）在电场中的运动的相关知识，掌握带电颗粒:如液滴、油滴、尘埃、小球等，除有说明或明确的暗示以外，一般都不能忽略重力；由于带电粒子在匀强电场中所受电场力与重力都是恒力，因此可以用两种方法处理:①正交分解法;②等效“重力”法，以及对洛伦兹力的理解，了解洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功．
