题目内容
5.在有空气阻力的情况下,将一物体由地面竖直上抛,当它上升至距离地面h1高度时,其动能与重力势能相等,当它下降至离地面h2高度时,其动能又恰好与重力势能相等,已知抛出后上升的最大高度为H,则( )| A. | h1>$\frac{H}{2}$,h2<$\frac{H}{2}$ | B. | h1>$\frac{H}{2}$,h2>$\frac{H}{2}$ | C. | h1<$\frac{H}{2}$,h2<$\frac{H}{2}$ | D. | h1<$\frac{H}{2}$,h2>$\frac{H}{2}$ |
分析 在上升过程中根据动能定理列出方程,再根据h1处动能和势能相等列式,联立方程即可求解,同理可求下落过程
解答 解:设抛出点为零势能面,在h1处动能和势能相等,则有:$\frac{1}{2}$mv2=mgh1…①
从h1处运动到最高点的过程中,根据动能定理得:
0-$\frac{1}{2}$mv2=-(mg+f)(H-h1)…②
由①②解得:
h1=$\frac{mg+f}{2mg+f}$H>$\frac{H}{2}$
同理在下降过程中有:
$\frac{1}{2}$mv2=mgh2…③
$\frac{1}{2}$mv2=(mg-f)(H-h2)…④
由③④得:
h2=$\frac{mg-f}{2mg-f}$H<$\frac{H}{2}$;故A正确,BCD错误,
故选:A
点评 本题主要考查了动能定理的直接应用,抓住阻力与运动方向始终相反,在整个运动过程中始终做负功,也可以利用牛顿第二定律,但需要分析每一过程的受力和运动,不如动能定理简单;

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
15.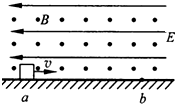 如图所示,一带正电荷的滑块以水平向右的初速度在粗糙水平面上滑动,匀强磁场垂直于纸面向外,匀强电场水平向左.滑块在水平面上经过a点后到b点时速度减为零,接着又滑了回来,滑块所带电荷量保持不变.则从a到b和从b回到a两过程相比较( )
如图所示,一带正电荷的滑块以水平向右的初速度在粗糙水平面上滑动,匀强磁场垂直于纸面向外,匀强电场水平向左.滑块在水平面上经过a点后到b点时速度减为零,接着又滑了回来,滑块所带电荷量保持不变.则从a到b和从b回到a两过程相比较( )
 如图所示,一带正电荷的滑块以水平向右的初速度在粗糙水平面上滑动,匀强磁场垂直于纸面向外,匀强电场水平向左.滑块在水平面上经过a点后到b点时速度减为零,接着又滑了回来,滑块所带电荷量保持不变.则从a到b和从b回到a两过程相比较( )
如图所示,一带正电荷的滑块以水平向右的初速度在粗糙水平面上滑动,匀强磁场垂直于纸面向外,匀强电场水平向左.滑块在水平面上经过a点后到b点时速度减为零,接着又滑了回来,滑块所带电荷量保持不变.则从a到b和从b回到a两过程相比较( )| A. | 滑块所受摩擦力大小相同 | B. | 滑块速度变化量大小相同 | ||
| C. | 滑块动能变化量大小相同 | D. | 滑块电势能变化量大小相同 |
16. 如图所示,一根长导线弯曲成如图所示形状,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )
如图所示,一根长导线弯曲成如图所示形状,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )
 如图所示,一根长导线弯曲成如图所示形状,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )
如图所示,一根长导线弯曲成如图所示形状,通以直流电I,正中间用绝缘线悬挂一金属环C,环与导线处于同一竖直平面内.在电流I增大的过程中,下列叙述正确的是( )| A. | 金属环中无感应电流产生 | |
| B. | 金属环中有顺时针方向的感应电流 | |
| C. | 悬挂金属环C的竖直线中的张力变大 | |
| D. | 金属环C以线为轴旋转 |
13. 如图,半径为R的圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以相同的速率v0通过P点进入磁场,不考虑粒子间的相互作用.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的$\frac{1}{3}$.则,下列说法中正确的是( )
如图,半径为R的圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以相同的速率v0通过P点进入磁场,不考虑粒子间的相互作用.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的$\frac{1}{3}$.则,下列说法中正确的是( )
 如图,半径为R的圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以相同的速率v0通过P点进入磁场,不考虑粒子间的相互作用.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的$\frac{1}{3}$.则,下列说法中正确的是( )
如图,半径为R的圆形区域内有一垂直纸面的匀强磁场,P为磁场边界上的一点.有无数带有同样电荷、具有同样质量的粒子在纸面内沿各个方向以相同的速率v0通过P点进入磁场,不考虑粒子间的相互作用.这些粒子射出边界的位置均处于边界的某一段弧上,这段圆弧的弧长是圆周长的$\frac{1}{3}$.则,下列说法中正确的是( )| A. | 该区域内磁场的磁感应强度的大小为$\frac{{2\sqrt{3}m{v_0}}}{3qR}$ | |
| B. | 该区域内磁场的磁感应强度的大小为$\frac{{\sqrt{3}m{v_0}}}{3qR}$ | |
| C. | 粒子在磁场中运动的半径为$\frac{{\sqrt{3}R}}{2}$ | |
| D. | 粒子在磁场中运动的最长时间为$\frac{{\sqrt{3}πR}}{{2{v_0}}}$ |
20. 如图所示的皮带传动装置,主动轮1的半径与从动轮2的半径之比R1:R2=2:1,A、B分别是两轮边缘上的点,假设皮带不打滑,则下列说法正确的是( )
如图所示的皮带传动装置,主动轮1的半径与从动轮2的半径之比R1:R2=2:1,A、B分别是两轮边缘上的点,假设皮带不打滑,则下列说法正确的是( )
 如图所示的皮带传动装置,主动轮1的半径与从动轮2的半径之比R1:R2=2:1,A、B分别是两轮边缘上的点,假设皮带不打滑,则下列说法正确的是( )
如图所示的皮带传动装置,主动轮1的半径与从动轮2的半径之比R1:R2=2:1,A、B分别是两轮边缘上的点,假设皮带不打滑,则下列说法正确的是( )| A. | A、B两点的线速度之比为vA:vB=1:2 | B. | A、B两点的线速度之比为vA:vB=2:1 | ||
| C. | A、B两点的角速度之比为ωA:ωB=1:2 | D. | A、B两点的角速度之比为ωA:ωB=1:1 |
10.关于简谐运动的各物理量,下列说法正确的是( )
| A. | 振幅就是最大位移 | B. | 周期频率成反比 | ||
| C. | 振幅越大,周期越小 | D. | 振幅越小,频率越小 |
17.如图所示的电路中,当滑动变阻器R2的滑动触头P向下滑动时( )


| A. | 电压表的读数减小 | B. | R1消耗的功率增大 | ||
| C. | 电容器C两端的电压增大 | D. | 电容器C两极板间的电场强度增大 |
 如图所示,平行金属导轨间距L=0.2m,导轨平面与水平面夹角θ=37°,方向垂直导轨平面向上的匀强磁场,磁感应强度B=1.0T,质量m=10g的金属棒ab垂直两导轨放置.其电阻r=1.0Ω,ab与导轨间的动摩擦因数μ=0.2.两导轨的上端与R=9.0Ω的电阻连接,导轨电阻不计(g=10m/s2,sin37°=0.6,cos37°=0.8),求:
如图所示,平行金属导轨间距L=0.2m,导轨平面与水平面夹角θ=37°,方向垂直导轨平面向上的匀强磁场,磁感应强度B=1.0T,质量m=10g的金属棒ab垂直两导轨放置.其电阻r=1.0Ω,ab与导轨间的动摩擦因数μ=0.2.两导轨的上端与R=9.0Ω的电阻连接,导轨电阻不计(g=10m/s2,sin37°=0.6,cos37°=0.8),求: 某同学表演魔术时,将一小型条形磁铁藏在自己的袖子里,然后对着一悬挂的金属小球指手画脚,结果小球在他神奇的功力下飘起来.假设当隐藏的小磁铁位于小球的左上方某一位置C(图中θ=37°)时,金属小球偏离竖直方向的夹角也是37°,如图所示,已知小球的质量为m=4.8kg,该同学(含磁铁)的质量为M=50kg(sin37°=0.6,cos37°=0.8,g=10m/s2)求此时:
某同学表演魔术时,将一小型条形磁铁藏在自己的袖子里,然后对着一悬挂的金属小球指手画脚,结果小球在他神奇的功力下飘起来.假设当隐藏的小磁铁位于小球的左上方某一位置C(图中θ=37°)时,金属小球偏离竖直方向的夹角也是37°,如图所示,已知小球的质量为m=4.8kg,该同学(含磁铁)的质量为M=50kg(sin37°=0.6,cos37°=0.8,g=10m/s2)求此时: