Question

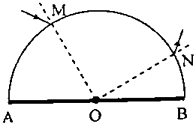
【题目】如图甲所示，以两虚线M、N为边界，中间存在平行纸面且与边界垂直的水平电场，M、N间电压UMN的变化图象如图乙所示，电压的最大值为U0、周期为T0；M、N两侧为相同的匀强磁场区域Ⅰ、Ⅱ，磁场方向垂直纸面向里，磁感应强度为B．t=0时，将一带正电的粒子从边界线M上的A处由静止释放，经电场加速后进入磁场，粒子在磁场中做圆周运动的周期也为T0 ． 两虚线M、N间宽度很小，粒子在其间的运动时间不计，也不考虑粒子所受的重力．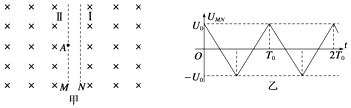

（1）求该粒子的比荷；
（2）求粒子第1次和第2次从右向左经边界线N离开磁场区域Ⅰ时两位置间的距离△d；
（3）若粒子的质量增加，电荷量不变，t=0时，将其在A处由静止释放，求t=2T0时粒子的速度．

Answer 1

【答案】
（1）解：粒子进入磁场后做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律得：qvB=m

粒子做圆周运动的周期为：T= ，

解得：R= ，T= ，周期与半径、速率无关，

由题可知：T=T0，解得： = ；

答：该粒子的比荷为 ；

（2）由于不计粒子穿越MN间的时间，则可认为t=0时刻出发的粒子穿越MN的过程中电压始终为U0，

t= T0时刻第1次自右向左穿过边界线N时再加速一次进入磁场区域Ⅱ时的速度为v1，

即区域ⅠⅡ匀速圆周运动一周时间T0共被加速2次，

由动能定理得：2qU0= mv12，

第2次自右向左到达边界线N（没到M）时被加速3次，速度设为v2，

由动能定理得：3qU0= mv22，

如右图所示，第1、2两次到达边界N的位置距离为△d：

△d=2（R2﹣R1）=2（ ﹣ ）

解得：△d=2（ ﹣ ） ；

答：粒子第1次和第2次从右向左经边界线N离开磁场区域Ⅰ时两位置间的距离△d为2（ ﹣ ） ；

（3）粒子的质量增加，粒子做圆周运动的周期：T′= ，

因为T0=则粒子匀速圆周运动的周期变为：T′=T0

匀速圆周运动的周期增加△T=T0

每半个周期为T=T0，增加T0

从t=0开始到t=2T0为止的时间内，根据加速电压图象可知粒子共加速了4次，

且加速电压分别为：U0、 U0、 U0、 U0

由动能定理得： mv2=q（1+ + + ）U0，

解得：v= = ；

答：若粒子的质量增加，电荷量不变，t=0时，将其在A处由静止释放，t=2T0时粒子的速度为 ．

【解析】（1）根据带电粒子，在匀强磁场中做匀速圆周运动，所需要的向心力由洛伦兹力提供，结合粒子在磁场中运动的周期公式求出粒子的比荷．
（2）第1次自右向左穿过边界线N后再加速一次进入磁场区域Ⅱ，共被加速2次；第2次自右向左穿过边界N时被加速3次，结合动能定理求出速度的大小，结合圆周运动的半径公式求出粒子第1次和第2次从右向左经边界线N离开磁场区域时两位置间的距离△d．
（3）根据粒子质量的变化，得出粒子在磁场中运动周期的变化，确定出粒子加速的次数和加速的电压大小，结合动能定理求出t=2T0时粒子的速度．