题目内容
18. 如图所示,半圆形玻璃砖的半径R=15cm,折射率为n=$\sqrt{3}$,直径AB与屏幕PQ垂直并接触于B点,OC与AB垂直,激光沿着与OC成i=30°角方向射向半圆形玻璃砖的圆心O,结果在屏幕PQ上出现两个光斑.
如图所示,半圆形玻璃砖的半径R=15cm,折射率为n=$\sqrt{3}$,直径AB与屏幕PQ垂直并接触于B点,OC与AB垂直,激光沿着与OC成i=30°角方向射向半圆形玻璃砖的圆心O,结果在屏幕PQ上出现两个光斑.(1)作出光路图(不考虑光沿原路返回);
(2)求两个光斑之间的距离;
(3)调整激光的入射方向,改变角度i的大小,使屏PQ上只剩一个光斑,求此光斑离B点的最长距离.
分析 (1)激光a射向半圆玻璃砖的圆心O,在AB面上产生了折射和反射,在屏幕MN上出现两个光斑,作出光路图.
(2)根据折射定律求出折射角.根据反射定律求出反射角,由几何关系求出两个光斑之间的距离L.
(3)入射角增大的过程中,当发生全反射时屏PQ上只剩一个光斑,此光斑离B最远时,恰好发生全反射,入射角等于临界角,由临界角公式和几何关系求解.
解答  解:(1)入射光线在AB面上一部分折射,还有一部分反射,光路图如图.
解:(1)入射光线在AB面上一部分折射,还有一部分反射,光路图如图.
(2)设折射角为r.
由折射定律得:n=$\frac{sinr}{sini}$,得:sinr=nsini=$\sqrt{3}$×sin30°=$\frac{\sqrt{3}}{2}$
得:r=60°
反射角i′=i=30°
由几何知识得△COD为直角三角形,所以两个光斑PQ之间的距离为:
L=CB+BD=Rtan30°+Rtan60°=(15×$\frac{\sqrt{3}}{3}$+15×$\sqrt{3}$)cm=20$\sqrt{3}$cm.
(3)在入射角增大的过程中,当发生全反射时屏PQ上只剩一个光斑,此光斑离A最远时,恰好发生全反射,入射角等于临界角:
i=C,则有:sinC=$\frac{1}{n}$=$\frac{\sqrt{3}}{3}$
可得 tanC=$\frac{\sqrt{2}}{2}$
此光斑离B点的最长距离为 S=$\frac{R}{tanC}$=15$\sqrt{2}$cm.
答:
(1)光路图如右图所示.
(2)两个光斑之间的距离为20$\sqrt{3}$cm.
(3)改变入射角,使屏PQ上只剩一个光斑,则此光斑离B点的最长距离为15$\sqrt{2}$ cm.
点评 关于几何光学的问题,关键是能正确的作出光路图.此题根据题意在水平屏幕MN上出现两个光斑是由于激光a在O点同时发生折射和反射形成的,作出光路图.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| 车速(km/h) | 反应距离(m) | 刹车距离(m) | 停车距离(m) |
| 60 | 15 | 22.5 | 37.5 |
| A. | 驾驶员的反应时间为0.6s | B. | 汽车的刹车时间为2.5s | ||
| C. | 汽车刹车的平均速度为$\frac{25}{3}$m/s | D. | 汽车刹车的加速度约为6m/s2 |
| A. | 水和酒精混合后总体积减小,说明分子间有空隙 | |
| B. | 当氢气和氧气的温度相同时,它们分子的平均速率相同 | |
| C. | 两铅块能被压合在一起,说明分子间存在引力 | |
| D. | 不浸润现象说明固体分子对液体分子的吸引力大于液体分子之间的吸引力 |
 在游乐节目中,选手需要借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角α=30°,绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6
在游乐节目中,选手需要借助悬挂在高处的绳飞越到水面的浮台上,小明和小阳观看后对此进行了讨论.如图所示,他们将选手简化为质量m=60kg的质点,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角α=30°,绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深.取重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6 如图所示,为一气体温度计的结构示意图,储有一定质量理想气体的测温泡P通过细管与水银压强计左臂A相连,压强计右管B和C之间通过软管相连,它们上端均与大气相通,大气压强等于75cmHg.当测温泡P浸在冰水混合物中,压强计左右A、C两管的水银面恰好都位于刻度尺的零刻度处,当将测温泡浸没在某液体中时,移动右管B调节A管内水银面的高度,使泡内气体体积不变,此时右管水银面的高度在15.0cm刻度处.求:此时被测液体的温度(大气压强保持恒定).
如图所示,为一气体温度计的结构示意图,储有一定质量理想气体的测温泡P通过细管与水银压强计左臂A相连,压强计右管B和C之间通过软管相连,它们上端均与大气相通,大气压强等于75cmHg.当测温泡P浸在冰水混合物中,压强计左右A、C两管的水银面恰好都位于刻度尺的零刻度处,当将测温泡浸没在某液体中时,移动右管B调节A管内水银面的高度,使泡内气体体积不变,此时右管水银面的高度在15.0cm刻度处.求:此时被测液体的温度(大气压强保持恒定).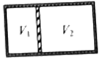 如图,气缸左右两侧气体由绝热活塞隔开,活塞与气缸光滑接触.初始时两侧气体均处于平衡态,体积之比V1:V2=1:2,温度之比T1:T2=2:5.先保持右侧气体温度不变,升高左侧气体温度,使两侧气体体积相同;然后使活塞导热,两侧气体最后达到平衡.求:
如图,气缸左右两侧气体由绝热活塞隔开,活塞与气缸光滑接触.初始时两侧气体均处于平衡态,体积之比V1:V2=1:2,温度之比T1:T2=2:5.先保持右侧气体温度不变,升高左侧气体温度,使两侧气体体积相同;然后使活塞导热,两侧气体最后达到平衡.求: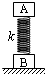 如图所示,A、B两个物块用轻弹簧相连接,它们的质量分别为mA=2kg和mB=3kg,弹簧的劲度系数为k=400N/m,物块B置于水平地面上,物块A靠弹簧托住,系统处于静止状态.现用一恒力F=60N竖直向上拉物块A使之向上运动,重力加速度g取10m/s2,试求:
如图所示,A、B两个物块用轻弹簧相连接,它们的质量分别为mA=2kg和mB=3kg,弹簧的劲度系数为k=400N/m,物块B置于水平地面上,物块A靠弹簧托住,系统处于静止状态.现用一恒力F=60N竖直向上拉物块A使之向上运动,重力加速度g取10m/s2,试求: