题目内容
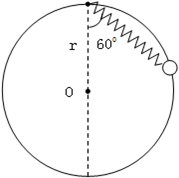如图所示，半径为r的光滑圆环竖直放置固定，将一轻质弹簧的一端固定在竖直直径的上端，另一端固定一质量为m，中间有孔的小球，光滑圆环从孔中穿过．当小球静止时，弹簧与竖直直径的夹角为60．已知弹簧原长为| r |
| 2 |
分析：对小球进行受力分析，小球受重力、弹簧弹力、圆环的支持力，根据几何关系求得三个力之间的关系，以及弹簧的长度，根据胡克定律求解弹簧的劲度系数．
解答：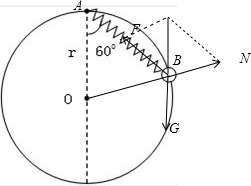
解：A、对小球进行受力分析，小球受重力、弹簧弹力、圆环的支持力，三个力作用，故A正确；
B、圆环对小球弹力的方向从圆心指向小球位置沿背离半径方向，故B错误；
C、根据几何知识可知，△OAB是等边三角形，所以F=N=G，弹簧的长度为r，故C正确；
D、根据胡克定律得：
F=kx
所以k=
=
，故D正确．
故选ACD
解：A、对小球进行受力分析，小球受重力、弹簧弹力、圆环的支持力，三个力作用，故A正确；B、圆环对小球弹力的方向从圆心指向小球位置沿背离半径方向，故B错误；
C、根据几何知识可知，△OAB是等边三角形，所以F=N=G，弹簧的长度为r，故C正确；
D、根据胡克定律得：
F=kx
所以k=
| mg | ||
|
| 2mg |
| r |
故选ACD
点评：本题主要考查了同学们受力分析的能力，要求同学们能正确对物体进行受力分析，根据力的合成与分解原则及几何关系求解，难度适中．
练习册系列答案
相关题目
如图所示，半径为R的光滑半圆轨道竖直放置，两个质量均为m的小球A、B以不同的速率进入轨道，A通过最高点C时，对轨道的压力为3mg，B通过最高点C时，对轨道的压力恰好为零，求：
如图所示，半径为R的vt-sB=l光滑圆弧轨道竖直放置，底端与光滑的水平轨道相接，质量为m的小球B静止光滑水平轨道上，其左侧连接了一轻质弹簧，质量为m的小球A自圆弧轨道的顶端由静止释放，重力加速度为g，小球可视为质点．
如图所示，半径为R的
如图所示，半径为R的半圆轨道BC竖直放置．一个质量为m 的小球以某一初速度从A点出发，经AB段进入半圆轨道，在B点时对轨道的压力为7mg，之后向上运动完成半个圆周运动恰好到达C点．试求：
如图所示，半径为r的圆筒，绕竖直中心轴OO′旋转，小物块a靠在圆筒的内壁上，它与圆筒内壁间的动摩擦因数为μ，现要使a不下落，则圆筒转动的角速度ω至少为（ ）