��Ŀ����
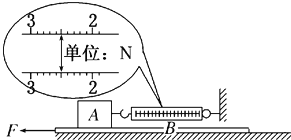
����Ŀ����ͼ��ʾ�����������ֵ����ͬһˮƽ���ϣ��������ߵ��е�ΪO����ֱ���ڵİ�Բ���⻬��Ե�����ֱ��ABˮƽ��Բ����O�㣬Բ���İ뾶ΪR��CΪԲ���ϵ�һ�㣬OCΪ��ֱ����ļн�Ϊ37�㣬һ�����Ϊ+q������Ϊm�Ĵ���С��ӹ����A���ɾ�ֹ�ͷţ��ع����������͵�ʱ���ٶ�v=2 ![]() ��gΪ�������ٶȣ�ȡ����Զ������Ϊ�㣬������˵����ȷ���ǣ� ��
��gΪ�������ٶȣ�ȡ����Զ������Ϊ�㣬������˵����ȷ���ǣ� ��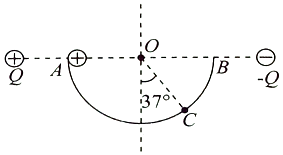
A.�糡��A��ĵ���Ϊ ![]()
B.�糡��B��ĵ���Ϊ ![]()
C.С���˶���B��ʱ�Ķ���Ϊ2mgR
D.С���˶���C��ʱ���䶯��������ܵĺ�Ϊ1.6mgR
���𰸡�A,C
���������⣺A��ȡ����Զ������Ϊ0������͵㴦����Ϊ0��С���A���˶�����͵�����У��ɶ��ܶ����ɵã�
![]()
��� ![]()
��UAO=��A��0
��ã� ![]() ����A��ȷ��
����A��ȷ��
B���ɶԳ��Կ�֪��UAO=UBO
������A��0=0����B
���� ![]() ����B����
����B����
C��С���A���˶���B������У��ɶ��ܶ����ã�
Ek=qUAB=2mgR����C��ȷ��
D��С������͵㴦�Ķ��ܺ͵����ܵ��ܺ�Ϊ�� ![]()
����͵��˶���C����̣����ܡ������ܡ��������ܵ������غ㣬����������������Ϊ����Ep=mgR��1��cos37�㣩=0.2mgR
�ʶ��ܡ������ܵ��ۺϼ�����0.2mgR������С����C��Ķ��ܺ͵����ܵ��ܺ�Ϊ��E2=E1��0.2mgR=1.8mgR����D����
��ѡ��AC
ͼ�й�O���������һ�������ߣ�һֱ���쵽����Զ��O��ĵ���Ϊ�㣮С���A�˶�����͵�Ĺ��̣��ɶ��ܶ������AO�����ĵ��Ʋ�Ӷ��õ�A��ĵ��ƣ��ɶԳ�����B��ĵ��ƣ�С�����͵㵽B�Ĺ��̣��������غ㶨����С���˶���B��ʱ�Ķ��ܣ��������������

 ��У����ϵ�д�
��У����ϵ�д�