题目内容
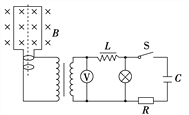
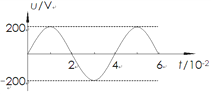
【题目】如图(甲)所示,平行光滑金属导轨水平放置,两轨相距L=0.4 m,导轨一端与阻值R=0.3Ω的电阻相连,导轨电阻不计。导轨x>0一侧存在沿x方向均匀增大的磁场,其方向与导轨平面垂直向下,磁感应强度B随位置x变化如图(乙)所示。一根质量m=0.2 kg、电阻r=0.1 Ω的金属棒置于导轨上,并与导轨垂直,棒在外力F作用下从x=0处以初速度v0=2m/s沿导轨向右变速运动,且金属棒在运动过程中受到的安培力大小不变。下列说法中正确的是( )
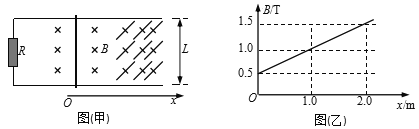
A. 金属棒向右做匀减速直线运动
B. 金属棒在x=1 m处的速度大小为0.5m/s
C. 金属棒从x=0运动到x=1m过程中,外力F所做的功为0.175 J
D. 金属棒从x=0运动到x=2m过程中,流过金属棒的电量为2C
【答案】BD
【解析】
A、根据图象得B﹣x函数关系式:![]()
金属棒向右运动切割磁感线产生感应电动势:![]()
感应电流:![]()
安培力:![]()
解得:![]()
根据匀变速直线运动的速度位移公式:![]() ,如果是匀变速直线运动,v2与x成线性关系,而由上式知,金属棒不可能做匀减速直线运动,A错误;
,如果是匀变速直线运动,v2与x成线性关系,而由上式知,金属棒不可能做匀减速直线运动,A错误;
B、根据题意金属棒所受的安培力大小不变,x=0处与x=1m处安培力大小相等,有![]() ,即
,即![]() ,B正确;
,B正确;
C、金属棒在x=0处的安培力大小为:![]()
对金属棒金属棒从x=0运动到x=1m过程中,根据动能定理有:
![]() ,
,
代入数据:![]()
解得:![]() ,C错误;
,C错误;
D、根据感应电量公式:![]()
x=0到x=2m过程中,B﹣x图象包围的面积:![]()
![]() ,D正确;
,D正确;
故选BD。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目