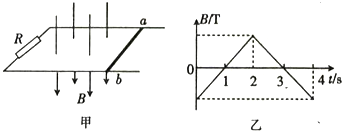
题目内容
20.一辆汽车做匀变速直线运动,初速度为10m/s,经2s速度达到了6m/s.问:(1)该汽车运动的加速度?
(2)这辆汽车在6s内发生的位移?
分析 根据加速度和时间求出速度变化量,结合速度时间公式求出第2s末的速度.根据速度时间公式求出汽车减为零的时间,判断汽车是否停止.
解答 解:(1)初速度为10m/s,经2s速度达到了6m/s,则:a=$\frac{v-{v}_{0}}{t}=\frac{6-10}{2}=-2m/{s}^{2}$
加速度是-2m/s 2,说明汽车做匀减速直线运动;
(2)假设汽车经过t′后停止,则:t′=$\frac{{v}_{t}-{v}_{0}}{a}=\frac{0-10}{-2}s=5s$,也就是说,汽车经过5s就停止了,6 s内的位移等于5s内的位移:
$x=\frac{0-{v}_{0}^{2}}{2a}=\frac{0-1{0}^{2}}{-2×2}=25$m
答:(1)该汽车运动的加速度是2m/s 2,方向与初速度的方向相反;
(2)这辆汽车在6s内发生的位移是25m.
点评 解决本题的关键掌握匀变速直线运动的速度时间公式,并能灵活运用,注意本题属于刹车问题,汽车速度减为零后不再运动.

练习册系列答案
相关题目
11.在物理学的重大发现中科学家们创造出了许多物理学方法,以下关于所用物理学研究方法的叙述正确的是( )
| A. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 | |
| B. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法 | |
| C. | 在定义加速度时,a=$\frac{△v}{△t}$,采用了比值定义法 | |
| D. | 在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
8.某同学探究弹力与弹簧伸长量的关系.
①将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在竖直方向(填“水平”或“竖直”)
②弹簧自然悬挂,待弹簧稳定时,长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如下表表:
表中有一个数值记录不规范,代表符号为L3.由表可知所用刻度尺的最小长度为1mm.
③图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与L1的差值(填“L0或L1”).
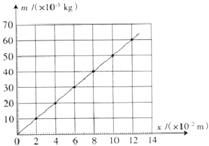
④由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g(结果保留两位有效数字,重力加速度取9.8m/s2).
①将弹簧悬挂在铁架台上,将刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都应在竖直方向(填“水平”或“竖直”)
②弹簧自然悬挂,待弹簧稳定时,长度记为L0,弹簧下端挂上砝码盘时,长度记为Lx;在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6,数据如下表表:
| 代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
| 数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 35.35 | 37.40 | 39.30 |
③图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与L1的差值(填“L0或L1”).

④由图可知弹簧的劲度系数为4.9N/m;通过图和表可知砝码盘的质量为10g(结果保留两位有效数字,重力加速度取9.8m/s2).
15.汽车甲、乙从A沿直线运动到B,甲以速度v0匀速直线运动从A到B,乙从A点由静止开始,以加速度大小为a1匀加速直线运动,接着又以加速度大小为a2匀减速直线运动到B时刚好静止,且甲、乙两车从A到B的时间相同,均为t,则( )
| A. | 乙车在运动过程中的最大速度与a1、a2有关 | |
| B. | A、B两点的长度为v0t | |
| C. | 不论a1、a2为何值,都有$\frac{{{a_1}{a_2}}}{{{a_1}+{a_2}}}=\frac{{2{v_0}}}{t}$ | |
| D. | 不论a1、a2为何值,都有$\frac{{{a_1}{a_2}}}{{{a_1}+{a_2}}}=\frac{v_0}{t}$ |
5.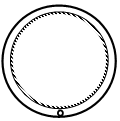 如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,外圆光滑,内圆粗糙.一质量为m的小球从轨道的最低点以初速度v0向右运动,球的直径略小于两圆间距,球运动的轨道半径为R,不计空气阻力.设小球过最低点时重力势能为零,下列说法正确的是( )
如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,外圆光滑,内圆粗糙.一质量为m的小球从轨道的最低点以初速度v0向右运动,球的直径略小于两圆间距,球运动的轨道半径为R,不计空气阻力.设小球过最低点时重力势能为零,下列说法正确的是( )
 如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,外圆光滑,内圆粗糙.一质量为m的小球从轨道的最低点以初速度v0向右运动,球的直径略小于两圆间距,球运动的轨道半径为R,不计空气阻力.设小球过最低点时重力势能为零,下列说法正确的是( )
如图所示,在竖直平面内固定有两个很靠近的同心圆轨道,外圆光滑,内圆粗糙.一质量为m的小球从轨道的最低点以初速度v0向右运动,球的直径略小于两圆间距,球运动的轨道半径为R,不计空气阻力.设小球过最低点时重力势能为零,下列说法正确的是( )| A. | 若小球运动到最高点时速度为0,则小球机械能一定不守恒 | |
| B. | 若经过足够长时间,小球最终的机械能可能为$\frac{3}{2}$mgR | |
| C. | 若使小球始终做完整的圆周运动,则v0一定不小于$\sqrt{5gR}$ | |
| D. | 若小球第一次运动到最高点时速度大小为0,则v0一定大于$\sqrt{4gR}$ |
9.操场上体重为40kg的小花在以5m/s的速度跑步;小强将质量为5kg的铅球以10m/s的速度抛出.则小花与铅球的动能之比为( )
| A. | 1:1 | B. | 2:1 | C. | 3:2 | D. | 4:1 |