题目内容
一质量为m=4.0×103 kg,发动机额定功率为P=60kW的汽车从静止开始以a=0.5m/s2的加速度做匀加速直线运动后以额定功率运动,它在运动中所受阻力为车重的0.1倍,g取10m/s2,求:
(1)起动后2s末发动机的输出功率;
(2)它以0.5m/s2的加速度做匀加速运动的时间;
(3)汽车在此路面上行驶的最大速度;
(4)若汽车经过100s时间速度达到最大值,求这段时间内汽车前进的距离.
(1)起动后2s末发动机的输出功率;
(2)它以0.5m/s2的加速度做匀加速运动的时间;
(3)汽车在此路面上行驶的最大速度;
(4)若汽车经过100s时间速度达到最大值,求这段时间内汽车前进的距离.
分析:(1)当汽车以额定功率做匀速运动时,速度最大,此时牵引力与阻力大小相等,由牵引力功率公式P=Fvm,求出阻力大小.汽车做匀加速直线运动过程中,由牵引力和阻力的合力产生加速度,根据牛顿第二定律求出牵引力.3s汽车的速度大小v=at,由P=Fv求解;
(2)汽车做匀加速运动过程中,当汽车的实际功率达到额定功率时,匀加速运动结束,由P=Fv求出匀加速运动的末速度,由v=at公式求解匀加速运动的时间;
(3)先求出汽车的速度为16m/s汽车的牵引力,再根据牛顿第二定律求解加速度.
(2)汽车做匀加速运动过程中,当汽车的实际功率达到额定功率时,匀加速运动结束,由P=Fv求出匀加速运动的末速度,由v=at公式求解匀加速运动的时间;
(3)先求出汽车的速度为16m/s汽车的牵引力,再根据牛顿第二定律求解加速度.
解答:解:(1)汽车受到的阻力位f=0.1mg=4000N
由牛顿第二定律可知
F-f=ma
F=f+ma=6000N
2s末的速度为
V=at1=0.5×2m/s=1m/s
起动后2s末发动机的输出功率P=FV=6kW
(2)汽车做匀加速运动过程中,当汽车的实际功率达到额定功率时,由P=Fv1得
匀加速运动的末速度v1=
=
m/s=10m/s
汽车做匀加速运动的时间t=
=
s=20s
(3)当牵引力等于阻力时速度达到最大
P=fVmax
Vmax=
=
m/s=15m/s
(4)匀加速阶段前进的位移为
x1=
at2=
×0.5×202=100m
达到额定功率后运动的时间为t′=t总-t=100s-20s=80s
由动能定理可知
Pt′-fx=
-
mv2
x=
=
m=1137.5m
所以经历的总位移为
X=x1+x=100m+1137.5m=1237.5m
答:(1)起动后2s末发动机的输出功率6kw;
(2)汽车做匀加速直线运动的时间是20s;
(3)汽车在此路面上行驶的最大速度15m;
(4)若汽车经过100s时间速度达到最大值,求这段时间内汽车前进的距离为1237.5m.
由牛顿第二定律可知
F-f=ma
F=f+ma=6000N
2s末的速度为
V=at1=0.5×2m/s=1m/s
起动后2s末发动机的输出功率P=FV=6kW
(2)汽车做匀加速运动过程中,当汽车的实际功率达到额定功率时,由P=Fv1得
匀加速运动的末速度v1=
| P |
| F |
| 60000 |
| 6000 |
汽车做匀加速运动的时间t=
| V1 |
| a |
| 10 |
| 0.5 |
(3)当牵引力等于阻力时速度达到最大
P=fVmax
Vmax=
| P |
| f |
| 60000 |
| 4000 |
(4)匀加速阶段前进的位移为
x1=
| 1 |
| 2 |
| 1 |
| 2 |
达到额定功率后运动的时间为t′=t总-t=100s-20s=80s
由动能定理可知
Pt′-fx=
| 1 |
| 2 |
| mv | 2 max |
| 1 |
| 2 |
x=
Pt′-
| ||||||
| f |
60000×80-
| ||||
| 4000 |
所以经历的总位移为
X=x1+x=100m+1137.5m=1237.5m
答:(1)起动后2s末发动机的输出功率6kw;
(2)汽车做匀加速直线运动的时间是20s;
(3)汽车在此路面上行驶的最大速度15m;
(4)若汽车经过100s时间速度达到最大值,求这段时间内汽车前进的距离为1237.5m.
点评:本题是交通工具的启动问题,关键抓住两点:一是汽车运动过程的分析;二是两个临界条件:匀加速运动结束和速度最大的条件.

练习册系列答案
相关题目
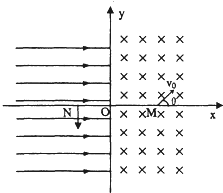 (2011?周口模拟)在xOy平面内,x>0的区域存在垂直纸面向里的匀强磁场,磁感应强度为B=0.4T;x<0的区域存在沿x轴正方向的匀强电场.现有一质量为m=4.0×10-9 kg,带电荷量为q=2.0×10-7 C的正粒子从x轴正方向上的M点以速度v0=20m/s进入磁场,如图所示,v0与x轴正方向的夹角θ=45°,M点与O点相距为l=
(2011?周口模拟)在xOy平面内,x>0的区域存在垂直纸面向里的匀强磁场,磁感应强度为B=0.4T;x<0的区域存在沿x轴正方向的匀强电场.现有一质量为m=4.0×10-9 kg,带电荷量为q=2.0×10-7 C的正粒子从x轴正方向上的M点以速度v0=20m/s进入磁场,如图所示,v0与x轴正方向的夹角θ=45°,M点与O点相距为l=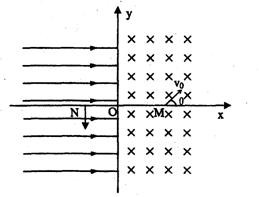 能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力。求:
能以沿着y轴负方向的速度垂直穿过x轴负半轴上的N点,不计粒子重力。求: