题目内容
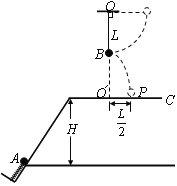
【题目】如图所示，在光滑的水平桌面上有体积相同的两个小球A、B，质量分别为m=0.1kg和M=0.3kg，两球中间夹着一根压缩的轻弹簧，原来处于静止状态，同时放开A、B球和弹簧，已知A球脱离弹簧的速度为6m/s，接着A球进入与水平面相切，半径为0.5m的竖直面内的光滑半圆形轨道运动，PQ为半圆形轨道竖直的直径，
，下列说法正确的是
A. 弹簧弹开过程，弹力对A的冲量大于对B的冲量
B. A球脱离弹簧时B球获得的速度大小为2m/s
C. A球从P点运动到Q点过程中所受合外力的冲量大小为1N·s
D. 若半圆轨道半径改为0.9m，则A球不能到达Q点
【答案】BCD
【解析】试题分析：根据弹簧对A、B的弹力大小关系、作用时间关系分析弹力对A、B冲量关系．弹簧弹开过程，根据动量守恒定律求A球脱离弹簧时B球获得的速度．由机械能守恒定律求A球到达Q点的速度，再由动量定理求A球从P点运动到Q点过程中所受合外力的冲量大小．若半圆轨道半径改为0.9m，求出A球到达Q点时的最小速度，再分析A球能否到达Q点．
弹簧弹开两小球的过程，弹力相等，作用时间相同，根据冲量定义可知，弹力对A的冲量大小等于B的冲量大小，A错误；由动量守恒定律
，解得A球脱离弹簧时B球获得的速度大小为
，B正确；设A球运动到Q点时速率为v，对A球从P点运动到Q点的过程，由机械能守恒定律可得
，解得v=4m/s，根据动量定理
，即A球从P点运动到Q点过程中所受合外力的冲量大小为1N·s，C正确；若半圆轨道半径改为0.9m，小球到达Q点的临界速度
，对A球从P点运动到Q点的过程，由机械能守恒定律，解得
，小于小球到达Q点的临界速度，则A球不能达到Q点，D正确．
练习册系列答案
相关题目
