题目内容
 倾角θ=37°的雪道长L=50m,高h=30m,下端经过一小段圆弧过渡后与很长的雪道相接,如图所示.一滑雪运动员在倾斜雪道顶端以水平速度v0=10m/s飞出,在浇到倾斜雪道上时,运动员靠改变姿态进行缓冲使自己只保留沿斜面的速度而不弹起.除缓冲外,运动员还可视为质点.过渡轨道光滑,其长度可忽略不计.设滑雪与雪道间的动摩擦因数μ=0.5,已知g=10m/s2,sin37°=0.6,cos37°=0.8.求:
倾角θ=37°的雪道长L=50m,高h=30m,下端经过一小段圆弧过渡后与很长的雪道相接,如图所示.一滑雪运动员在倾斜雪道顶端以水平速度v0=10m/s飞出,在浇到倾斜雪道上时,运动员靠改变姿态进行缓冲使自己只保留沿斜面的速度而不弹起.除缓冲外,运动员还可视为质点.过渡轨道光滑,其长度可忽略不计.设滑雪与雪道间的动摩擦因数μ=0.5,已知g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)运动员落在倾斜雪道上时与飞出点间的距离;
(2)运动员落到倾斜雪道瞬间沿斜面的速度大小;
(3)运动员在水平雪道上滑行的距离.
分析:(1)根据位移方向列方程,得到时间t,再计算射程和下降的高度,最后合成合位移S;
(2)根据速度的合成与分解的平行四边形定则,结合几何关系得到运动员沿斜面方向的速度;
(3)对加速过程运用牛顿第二定律和速度位移公式列式,再对运动员在水平面上的运动运用动能定理列式,最后连列方程组求解.
(2)根据速度的合成与分解的平行四边形定则,结合几何关系得到运动员沿斜面方向的速度;
(3)对加速过程运用牛顿第二定律和速度位移公式列式,再对运动员在水平面上的运动运用动能定理列式,最后连列方程组求解.
解答:解:(1)运动员落到斜面上的P点:tanθ=
①
代入数据得t=1.5s②
水平距离x=v0t得
OP间距离s=
③
代入数据得s=18.75m④
(2)落到P点有:vy=gt
v斜=v0cosθ+vysinθ⑤
代入数据得v斜=17m/s⑥
(3)运动员在斜面上的加速度a=gsinθ-μgcosθ⑦
运动员在斜面末端速度
=
+2a(L-s)⑧
运动员在水平雪道上滑行的距离有:-μmgLx=0-
m
⑨
代入数据得Lx=196.3m⑩
答:(1)运动员落在倾斜雪道上时与飞出点间的距离是18.75m;
(2)运动员落到倾斜雪道瞬间沿斜面的速度大小是17m/s;
(3)运动员在水平雪道上滑行的距离是196.3m.
| ||
| v0t |
代入数据得t=1.5s②
水平距离x=v0t得
OP间距离s=
| x |
| cosθ |
代入数据得s=18.75m④
(2)落到P点有:vy=gt
v斜=v0cosθ+vysinθ⑤
代入数据得v斜=17m/s⑥
(3)运动员在斜面上的加速度a=gsinθ-μgcosθ⑦
运动员在斜面末端速度
| v | 2 1 |
| v | 2 斜 |
运动员在水平雪道上滑行的距离有:-μmgLx=0-
| 1 |
| 2 |
| v | 2 1 |
代入数据得Lx=196.3m⑩
答:(1)运动员落在倾斜雪道上时与飞出点间的距离是18.75m;
(2)运动员落到倾斜雪道瞬间沿斜面的速度大小是17m/s;
(3)运动员在水平雪道上滑行的距离是196.3m.
点评:本题关键将平抛运动过程沿水平和竖直方向正交分解,根据合位移方向列式求出平抛运动的时间,然后对加速过程和减速过程运用动能定理、运动学公式列式联立求解.

练习册系列答案
相关题目
 如图所示,ABC是一雪道,AB段为长L=80m倾角θ=37°的斜坡,BC段水平,AB与BC平滑相连.一个质量m=75kg的滑雪运动员,从斜坡顶端以v0=2.0m/s的初速度匀加速滑下,经时间t=5.0s 到达斜坡底端B点.滑雪板与雪道间的动摩擦因数在AB段和BC段均相同.取g=10m/s2.(sin37°=0.6,cos37°=0.8).求:
如图所示,ABC是一雪道,AB段为长L=80m倾角θ=37°的斜坡,BC段水平,AB与BC平滑相连.一个质量m=75kg的滑雪运动员,从斜坡顶端以v0=2.0m/s的初速度匀加速滑下,经时间t=5.0s 到达斜坡底端B点.滑雪板与雪道间的动摩擦因数在AB段和BC段均相同.取g=10m/s2.(sin37°=0.6,cos37°=0.8).求: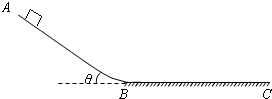 如图,AB段为长L=8m倾角θ=37°的斜面,BC段水平,AB与BC平滑相连.一个质量m=2kg的物体从斜坡顶端以v0=2.0m/s的初速度匀加速滑下,经时间t=2.0s 到达斜坡底端B点.滑雪板与雪道间的动摩擦因数在AB段和BC段均相同.求:
如图,AB段为长L=8m倾角θ=37°的斜面,BC段水平,AB与BC平滑相连.一个质量m=2kg的物体从斜坡顶端以v0=2.0m/s的初速度匀加速滑下,经时间t=2.0s 到达斜坡底端B点.滑雪板与雪道间的动摩擦因数在AB段和BC段均相同.求: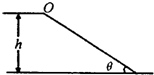 在2010年温哥华冬季奥运会中滑雪比赛惊险刺激,倾角θ=37°的雪道长L=50m,高h=30m,下端经过一小段圆弧过渡后与很长的雪道相接,如图所示.一滑雪运动员在倾斜雪道顶端以水平速度v0=10m/s飞出,在落到倾斜雪道上时,运动员靠改变姿态进行缓冲使自己只保留沿斜面的速度而不弹起.除缓冲外,运动员还可视为质点.过渡轨道光滑,其长度可忽略不计.设运动员在水平雪道上滑行的距离为196.3m,已知g=10m/s2,sin37°=0.6,cos37°=0.8.
在2010年温哥华冬季奥运会中滑雪比赛惊险刺激,倾角θ=37°的雪道长L=50m,高h=30m,下端经过一小段圆弧过渡后与很长的雪道相接,如图所示.一滑雪运动员在倾斜雪道顶端以水平速度v0=10m/s飞出,在落到倾斜雪道上时,运动员靠改变姿态进行缓冲使自己只保留沿斜面的速度而不弹起.除缓冲外,运动员还可视为质点.过渡轨道光滑,其长度可忽略不计.设运动员在水平雪道上滑行的距离为196.3m,已知g=10m/s2,sin37°=0.6,cos37°=0.8.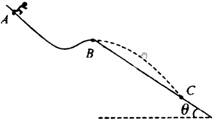 如图,质量m=60kg的高山滑雪运动员,从A点山静止开始沿雪道滑下,从B点水平飞出后又落在与水平面成倾角θ=37°的斜坡上C点.己知AB两点间的高度差为h=25m,B、C两点间的距离为S=75m,(g取l0m/s2 sin37°=0.6,cos37°=0.8),求:
如图,质量m=60kg的高山滑雪运动员,从A点山静止开始沿雪道滑下,从B点水平飞出后又落在与水平面成倾角θ=37°的斜坡上C点.己知AB两点间的高度差为h=25m,B、C两点间的距离为S=75m,(g取l0m/s2 sin37°=0.6,cos37°=0.8),求: