题目内容
 如图所示,ABC是一雪道,AB段为长L=80m倾角θ=37°的斜坡,BC段水平,AB与BC平滑相连.一个质量m=75kg的滑雪运动员,从斜坡顶端以v0=2.0m/s的初速度匀加速滑下,经时间t=5.0s 到达斜坡底端B点.滑雪板与雪道间的动摩擦因数在AB段和BC段均相同.取g=10m/s2.(sin37°=0.6,cos37°=0.8).求:
如图所示,ABC是一雪道,AB段为长L=80m倾角θ=37°的斜坡,BC段水平,AB与BC平滑相连.一个质量m=75kg的滑雪运动员,从斜坡顶端以v0=2.0m/s的初速度匀加速滑下,经时间t=5.0s 到达斜坡底端B点.滑雪板与雪道间的动摩擦因数在AB段和BC段均相同.取g=10m/s2.(sin37°=0.6,cos37°=0.8).求:(1)运动员在斜坡上滑行时加速度的大小a;
(2)滑雪板与雪道间的动摩擦因数μ;
(3)运动员滑上水平雪道后,在t'=2.0s内滑行的距离x.
分析:(1)根据匀变速直线运动的位移公式求出运动员的加速度.
(2)对斜坡上运动员受力分析,通过牛顿第二定律求出动摩擦因数的大小.
(3)根据牛顿第二定律求出水平轨道上运动员的加速度,通过位移时间公式求出运动员在水平雪道上滑行的距离.
(2)对斜坡上运动员受力分析,通过牛顿第二定律求出动摩擦因数的大小.
(3)根据牛顿第二定律求出水平轨道上运动员的加速度,通过位移时间公式求出运动员在水平雪道上滑行的距离.
解答: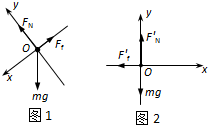 解:(1)根据 L=v0t+
解:(1)根据 L=v0t+
at2
解得 a=5.6m/s2
(2)在斜坡上运动员受力如图1所示
建立如图1所示的直角坐标系,根据牛顿第二定律
x方向 mgsinθ-Ff=ma
y方向 FN-mgcosθ=0
摩擦力 Ff=?FN
解得 ?=0.05
(3)运动员滑到B点时的速度 vB=v0+at=30m/s
在水平雪道上运动员受力如图2所示,设运动员的加速度为a'
建立如图2所示的直角坐标系,根据牛顿第二定律
x方向-?F'N=ma'
y方向 F'N-mg=0
根据 x=vBt′-
a′t′2
解得 x=59m
答:(1)运动员在斜坡上滑行时加速度的大小为5.6m/s2.
(2)滑雪板与雪道间的动摩擦因数为0.05.
(3)运动员滑上水平雪道后滑行的距离59m.
 解:(1)根据 L=v0t+
解:(1)根据 L=v0t+| 1 |
| 2 |
解得 a=5.6m/s2
(2)在斜坡上运动员受力如图1所示
建立如图1所示的直角坐标系,根据牛顿第二定律
x方向 mgsinθ-Ff=ma
y方向 FN-mgcosθ=0
摩擦力 Ff=?FN
解得 ?=0.05
(3)运动员滑到B点时的速度 vB=v0+at=30m/s
在水平雪道上运动员受力如图2所示,设运动员的加速度为a'
建立如图2所示的直角坐标系,根据牛顿第二定律
x方向-?F'N=ma'
y方向 F'N-mg=0
根据 x=vBt′-
| 1 |
| 2 |
解得 x=59m
答:(1)运动员在斜坡上滑行时加速度的大小为5.6m/s2.
(2)滑雪板与雪道间的动摩擦因数为0.05.
(3)运动员滑上水平雪道后滑行的距离59m.
点评:本题考查牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
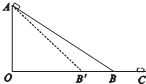 如图所示,ABC是一条长轨道,斜面和水平面摩擦因素相同,一质量为m的木块(可视为质点),在A点由静止释放,最后停在C点;现在改变斜面的倾角,如图中虚线AB'所示,仍从A点由静止释放该小木块,则木块最终将停放在(不计木块通过转折点B点或B'点的能量损失)( )
如图所示,ABC是一条长轨道,斜面和水平面摩擦因素相同,一质量为m的木块(可视为质点),在A点由静止释放,最后停在C点;现在改变斜面的倾角,如图中虚线AB'所示,仍从A点由静止释放该小木块,则木块最终将停放在(不计木块通过转折点B点或B'点的能量损失)( )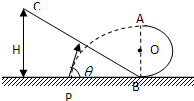 如图所示,ABC是一条由半圆和一段斜面组成的光滑轨道,A、B两点在同一竖直线上,且已知半圆半径为R,今在水平面某一点P处抛出一个小球,使它恰好从A点进入轨道,在B点处无能量损失,最后沿斜面上升到高度为H处,试求小球抛出点P的位置,抛射速度V及抛射角θ
如图所示,ABC是一条由半圆和一段斜面组成的光滑轨道,A、B两点在同一竖直线上,且已知半圆半径为R,今在水平面某一点P处抛出一个小球,使它恰好从A点进入轨道,在B点处无能量损失,最后沿斜面上升到高度为H处,试求小球抛出点P的位置,抛射速度V及抛射角θ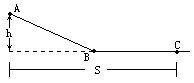 如图所示,ABC是一条滑道,滑雪者从A点由静止开始沿倾斜滑道AB滑下,然后又沿水平滑道BC滑行,最后停在C点.已知A点距水平面的高度为h,A点跟C点间的水平距离为s.试证明:滑雪板跟滑道间的动摩擦因数μ=h/s.
如图所示,ABC是一条滑道,滑雪者从A点由静止开始沿倾斜滑道AB滑下,然后又沿水平滑道BC滑行,最后停在C点.已知A点距水平面的高度为h,A点跟C点间的水平距离为s.试证明:滑雪板跟滑道间的动摩擦因数μ=h/s. (不计空气阻力)。
(不计空气阻力)。