题目内容
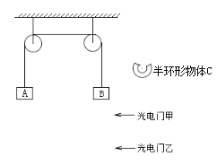
【题目】如图所示,轻弹簧一端固定于倾角为θ(θ<45°)的光滑斜面(固定)上方的O点,O点到斜面的距离OQ等于弹簧的原长L,弹簧另一端与小滑块(可视为质点)连接。在斜面上移动滑块至P点,使弹簧处于水平状态。现将滑块从P点由静止释放,滑块沿斜面运动到O点正下方M点,该过程中弹簧始终在弹性限度内。重力加速度大小为g。下列说法正确的是
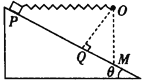
A. 滑块经过Q点时的速度最大
B. 滑块经过M点时的速度大于![]()
C. 滑块从P点运动到Q点的过程中,其加速度一直在减小
D. 滑块从P点运动到Q点过程动能的增量比Q点运动到M点过程动能的增量小
【答案】BC
【解析】
滑块在下滑过程中分析受力如何变化即可判断加速度和速度的变化情况,根据动能定理可以分析AB段和BC段动能增量的关系,同时结合几何关系判断弹簧弹力做功可得分析C点速度关系。
AC、滑块下滑过程中受到重力,斜面对它的支持力,还有弹簧弹力。在Q点弹簧恰处于原长且与斜面垂直,则滑块从P到Q合外力变小沿斜面向下,做加速度变小的加速运动。滑块从Q到M弹簧弹力变大,此过程中有可能合力一直沿斜面向下,那么滑块继续做加速度变小的加速运动;也有可能有合力向上的阶段,那么滑块在此阶段就做加速度先变小后变大的先加速后减速的运动。故A错误、C正确。
BD、弹簧原长为L,斜面倾角θ小于45°,由几何关系P到Q下降的高度差大于Q到M的高度差,又P到Q弹簧弹力对滑块做正功、Q到M做负功,根据动能定理P到Q阶段动能增加量大于Q到M阶段;设整个过程弹力做功为W,到达M点时速度为v,则由动能定理:![]() W
W![]() ,可得M点速度大于
,可得M点速度大于![]() ,故B正确,D错误。
,故B正确,D错误。

练习册系列答案
相关题目