题目内容
如图所示，固定在小车上的折杆∠A=θ，B端固定一个质量为m的小球，若车向右的加速度为a，则AB杆对小球的作用力F为（ ）分析：对球受力分析，可知其受重力，杆的作用力F，由力的合成的三角形定则可以知道判定F的大小，由此可以判定各个选项．
解答：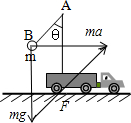
解：
由球只受重力和杆的作用力，由于合力一定沿水平方向，分力和合力构成直角三角形，如图：
故利用矢量合成的三角形定则，可知：F2=（mg）2+（ma）2，解得：F=m
，拉力的方向与竖直的夹角为α：tanα=
=
，可见夹角与加速度的大小有关，不一定就等于θ，故拉力方向不一定沿杆．
a=0时，F=mg，故A错误，
a=gtanθ时，F=mg
=
，故B错误
故ABC错误，D正确
故选D
解：由球只受重力和杆的作用力，由于合力一定沿水平方向，分力和合力构成直角三角形，如图：
故利用矢量合成的三角形定则，可知：F2=（mg）2+（ma）2，解得：F=m
| g2+a2 |
| ma |
| mg |
| a |
| g |
a=0时，F=mg，故A错误，
a=gtanθ时，F=mg
| 1+tanθ2 |
| mg |
| cosθ |
故ABC错误，D正确
故选D
点评：本题关键就是应用好力的合成的闭合三角形定则，若想着用力的分解，然后列平衡方程和牛顿第二定律，就走向误区了，本题就非常棘手了，这就是解题的技巧问题，需要对题目综合考量，选择一个最合适的解题方式．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如图所示，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆下端固定有质量为m的小球，下列关于杆对球的作用力F的判断中，正确的是（ ）
如图所示，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆下端固定有质量为m的小球，下列关于杆对球的作用力F的判断中，正确的是（ ）
如图所示，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆下端固定有质量为m的小球，
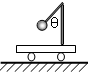如图所示，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆下端固定有质量为m的小球，下列关于杆对球的作用力F的判断中，正确的是（ ）| A、小车静止时，F=mg，方向竖直向上 | ||
| B、小车静止时，F=mgcosθ，方向垂直杆向上 | ||
| C、小车向右以加速度a运动时，一定有F=ma/sinθ． | ||
D、小车向左以加速度a运动时，F=
|