题目内容
 如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,
如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,(1)求小车静止时,杆对小球的作用力
(2)小车向左以加速度a加速运动时,杆对小球的作用力.
分析:(1)小球处于静止状态,合力为零,受力分析后根据平衡条件列式求解;
(2)先对小球受力分析,然后根据牛顿第二定律列求解.
(2)先对小球受力分析,然后根据牛顿第二定律列求解.
解答:解:(1)对小球受力分析,受重力和杆的弹力;
由于小球保持静止状态,合力为零,故弹力向上,大小等于mg;
 (2)对小球受力分析,受重力和杆的弹力F,如图;
(2)对小球受力分析,受重力和杆的弹力F,如图;
小球向左做加速运动,根据牛顿第二定律,有:
F1=ma
F2-mg=0
故:F=
,
方向斜向左上方,与竖直方向的夹角为:θ=arctan
=arctan
;
答:(1)求小车静止时,杆对小球的作用力为mg,方向竖直向上;
(2)小车向左以加速度a加速运动时,杆对小球的作用力为
,方向与竖直方向的夹角为arctan
.
由于小球保持静止状态,合力为零,故弹力向上,大小等于mg;
 (2)对小球受力分析,受重力和杆的弹力F,如图;
(2)对小球受力分析,受重力和杆的弹力F,如图;小球向左做加速运动,根据牛顿第二定律,有:
F1=ma
F2-mg=0
故:F=
|
| (ma)2+(mg)2 |
方向斜向左上方,与竖直方向的夹角为:θ=arctan
| F2 |
| F1 |
| g |
| a |
答:(1)求小车静止时,杆对小球的作用力为mg,方向竖直向上;
(2)小车向左以加速度a加速运动时,杆对小球的作用力为
| (ma)2+(mg)2 |
| g |
| a |
点评:本题关键是要明确杆的弹力与细线的弹力不同,杆的弹力可以与杆平行,也可以与杆不平行,可以是拉力,也可以是支持力.

练习册系列答案
相关题目
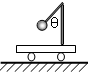 如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )
如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )| A、小车静止时,F=mg,方向竖直向上 | ||
| B、小车静止时,F=mgcosθ,方向垂直杆向上 | ||
| C、小车向右以加速度a运动时,一定有F=ma/sinθ. | ||
D、小车向左以加速度a运动时,F=
|
 如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )
如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( ) 如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( )
如图所示,固定在小车上的支架的斜杆与竖直杆的夹角为θ,在斜杆下端固定有质量为m的小球,下列关于杆对球的作用力F的判断中,正确的是( ) 如图所示,固定在小车上的折杆∠A=θ,B端固定一个质量为m的小球,若小车向右的加速度为a,AB杆对小球的作用力为F,则( )
如图所示,固定在小车上的折杆∠A=θ,B端固定一个质量为m的小球,若小车向右的加速度为a,AB杆对小球的作用力为F,则( )