题目内容
（A）．设地球的质量为M，半径为R，则环绕地球飞行的第一宇宙速度v的表达式为______________；某行星的质量约为地球质量的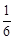
，半径约为地球半径的
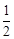，那么在此行星上的“第一宇宙速度”与地球上的第一宇宙速度之比为______________（已知万有引力常量为G）。
（B）．质量分别为60kg和70kg的甲、乙两人，分别同时从原来静止在光滑水平面上的小车两端.以3m/s的水平初速度沿相反方向跳到地面上。若小车的质量为20kg，则当两人跳离小车后，小车的运动速度大小为______________m/s，方向与______________（选填“甲”、“乙”）的初速度方向相同。
【答案】
A．v=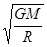
，
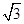/3︰1 (B)．1.5m/s，甲
【解析】
试题分析：在地球表面飞行时，重力可近似等于地球对物体的万有引力，故根据公式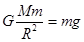
可得
，由此可得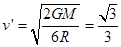
设甲运动的方向为正方向，跳之间，甲乙和小车组成的系统动量为零，跳后，系统受到的外力做功为零，所以动量守恒，故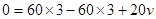
，解得
，方向为正，即和甲的运动方向相同，
考点：考查了动量守恒的应用
点评：做本题时，因为涉及到两个方向上的运动，所以需要选择正方向，然后根据动量守恒列等式求解
练习册系列答案
相关题目
设地球的质量为M，半径为R，自转的角速度为ω，地球表面的重力加速度为g，万有引力恒量为G，同步卫星轨道半径为r，则同步卫星的速度为（ ）
A、v=
| ||||
| B、v=ωr | ||||
C、v=
| ||||
D、v=
|
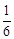，半径约为地球半径的
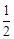，那么在此行星上的“第一宇宙速度”与地球上的第一宇宙速度之比为______________（已知万有引力常量为G）。