题目内容

设地球的质量为M，半径为R，自转的角速度为ω，地球表面的重力加速度为g，万有引力恒量为G，同步卫星轨道半径为r，则同步卫星的速度为（　　）
A、v=
rg
B、v=ωr
C、v=
GM
r
D、v=
GM
ω
分析：研究同步卫星绕地球做匀速圆周运动，根据万有引力提供向心力，列出等式求出线速度大小；也可以根据线速度定义求出线速度大小．
解答：解：A、由万有引力提供向心力，即
GMm
r2
=
mv2
r

在地球表面处物体万有引力等于重力得：
GMm
R2
=mg
联立解得：v=
GM
r
=
gR2
r
，故A错误，C正确；
B、同步卫星与地球同步，具有相同的角速度做匀速圆周运动，
则根据线速度和角速度关系可得：v=ωr，故B正确，D错误；
故选：BC．
点评：本题考查了万有引力在天体中的应用，解题的关键在于找出向心力的来源，并能列出等式解题．
万有引力定律得应用要结合圆周运动的知识解决问题．
练习册系列答案
相关题目
神舟五号载人飞船进入太空，标志着我国的太空实验研究进入了一个新的阶段．我国目前有西昌、太原、酒泉三个卫星发射中心，现正在海南岛新建第四个卫星发射中心．
（1）为了充分利用地球自转的速度，人造卫星发射时，火箭都是从西向东发射的．考虑这个因素，火箭发射场应建在纬度较
低
低
填高或低）的地方较好．
（2）关于人造地球卫星及其中物体的超重、失重问题，下列说法中不正确的是
AC
AC

A．在发射过程中向上加速时产生超重现象
B．在降落过程中向下减速时产生失重现象
C．进入轨道时作匀速圆周运动时，产生完全失重现象
D．失重是由于地球对卫星内物体作用力减小而引起的
（3）在进入圆轨道的空间实验室里，能进行的实验操作有
B
B
．
A．用弹簧秤测重力            B．用水银温度计测温度
C．用天平测质量            　D．用钩码探究弹力和弹簧伸长的关系
（4）火箭发射卫星的开始阶段是竖直升空，设向上的加速度为a=5m/s2，卫星中用弹簧秤悬挂一个质量m=9kg的物体．当卫星升空到某高处时，弹簧秤的示数为85N，那么此时卫星距地面的高度是多少千米？（地球半径取R=6400km，g=10m/s2）
（2009?天津）2008年12月，天文学家们通过观测的数据确认了银河系中央的黑洞“人马座A*”的质量与太阳质量的倍数关系．研究发现，有一星体S2绕人马座A*做椭圆运动，其轨道半长轴为9.50×102天文单位（地球公转轨道的半径为一个天文单位），人马座A*就处在该椭圆的一个焦点上．观测得到S2星的运行周期为15.2年．
（1）若将S2星的运行轨道视为半径r=9.50×102天文单位的圆轨道，试估算人马座A*的质量MA是太阳质量Ms的多少倍（结果保留一位有效数字）；
（2）黑洞的第二宇宙速度极大，处于黑洞表面的粒子即使以光速运动，其具有的动能也不足以克服黑洞对它的引力束缚．由于引力的作用，黑洞表面处质量为m的粒子具有势能为Ep=-G
MmR
（设粒子在离黑洞无限远处的势能为零），式中M、R分别表示黑洞的质量和半径．已知引力常量G=6.7×10-11N?m2/kg2，光速c=3.0×108m/s，太阳质量Ms=2.0×1030kg，太阳半径Rs=7.0×108m，不考虑相对论效应，利用上问结果，在经典力学范围内求人马座A*的半径RA与太阳半径Rg之比应小于多少（结果按四舍五入保留整数）．
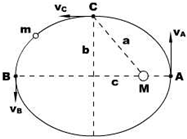精英家教网我国航天技术世界领先，天宫、神八相继发射成功，由此激发了我们对地球运动的深入研究．设地球和太阳的质量分别为m和M，地球绕太阳作椭圆运动，轨道的半长轴为a，半短轴为b，如图所示．（已知：地球的势能为-
GMmr
其中r是地球与太阳的距离），试求
（1）由能量与行星运动规律写出，地球在椭圆顶点A、B、C三点的运动速度vA，vB，vC有关的方程组．
（2）由（1）有关的方程组求出地球在椭圆顶点A、B、C三点的运动速度vA，vB，vC．
（3）求出地球运动轨迹在A、C两点的曲率半径ρA、ρC．
（以上有关结果由G、M、m、a、b表示）

（14分）

 

（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即，k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理，请你推导出太阳系中该常量k的表达式。已知引力常量为G，太阳的质量为M太。

（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立。经测定月地距离为3.84×108m，月球绕地球运动的周期为2.36×106S，试计算地球的质M地。（G=6.67×10-11Nm2/kg2，结果保留一位有效数字）

【解析】：（1）因行星绕太阳作匀速圆周运动，于是轨道的半长轴a即为轨道半径r。根据万有引力定律和牛顿第二定律有

                            ①

    于是有                           ②

即                                ③

（2）在月地系统中，设月球绕地球运动的轨道半径为R，周期为T，由②式可得

                                ④

解得     M地=6×1024kg                         ⑤

（M地=5×1024kg也算对）

23．【题文】（16分）

     如图所示，在以坐标原点O为圆心、半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t0时间从P点射出。

（1）求电场强度的大小和方向。

（2）若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。

（3）若仅撤去电场，带电粒子仍从O点射入，且速度为原来的4倍，求粒子在磁场中运动的时间。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网