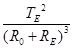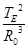题目内容
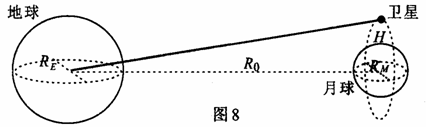
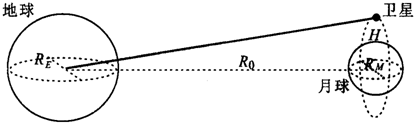
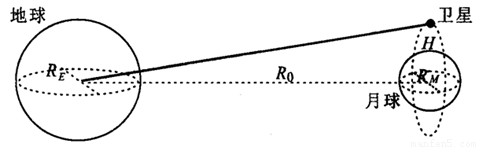
我国发射的探月卫星有一类为绕月极地卫星.利用该卫星可对月球进行成像探测.如图所示,设卫星在绕月极地轨道上做圆周运动时距月球表面的高度为H,绕行周期为TM; 月球绕地球公转的周期为TE,公转轨道半径为R0;地球半径为RE,月球半径为RM.忽略地球引力、太阳引力对绕月卫星的影响,则下列说法正确的是( )

分析:卫星绕月做圆周运动时,由月球的万有引力提供向心力,知道距月球表面高为H,月球半径为RM,绕行的周期为TM,根据由牛顿第二定律可求出月球的质量.月球绕地球公转时,由地球的万有引力提供向心力,由月球公转的周期为TE,半径为R0.地球半径为RE,根据由牛顿第二定律可求出地球的质量;根据几何知识求出卫星到地面最短距离,再求出时间;明确开普勒第三定律只适用于绕同一个中心天体运动,不同轨道和周期的关系式.
解答:解:A、根据天体间的运动,万有引力提供向心力,F万=m
,分别可求得地球的质量和月球的质量,即M月:M地=
,故A正确.
B、设探月极地轨道上卫星到地心的距离为L0,则卫星到地面最短距离为L0-RE,由几何知识得:
L02=R02+(RM+H)2
将照片发回地面的时间t=
=
,故B正确.
CD、由于开普勒第三定律只适用于绕同一个中心天体运动,TM和TE对应的中心天体分别是月球和地球,所以CD选项的表达式错误,故CD错误.
故选:AB.
| 4π2r |
| T2 |
| ||||
|
B、设探月极地轨道上卫星到地心的距离为L0,则卫星到地面最短距离为L0-RE,由几何知识得:
L02=R02+(RM+H)2
将照片发回地面的时间t=
| L0-RE |
| c |
| ||
| c |
CD、由于开普勒第三定律只适用于绕同一个中心天体运动,TM和TE对应的中心天体分别是月球和地球,所以CD选项的表达式错误,故CD错误.
故选:AB.
点评:本题是研究天体间的运动,利用万有引力与圆周运动知识的结合求解(万有引力提供向心力)是常用方法之一;明确开普勒第三定律只适用于绕同一个中心天体运动.

练习册系列答案
相关题目
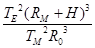
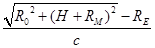
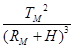 =
=