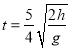Question

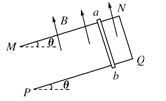
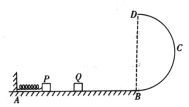
【题目】现将一弹簧水平放置，一端固定在A点，另一端与物块P接触但不连接。AB是长度为5的光滑水平轨道，B端与半径为的光滑半圆轨道BCD相切，半圆的直径BD竖直，如图所示。用外力推动质量为m物块P，将弹簧压缩至长度，具有的弹性势能为然后释放，P开始沿轨道运动，当弹簧恢复原长时，P与物体Q发生弹性正碰。重力加速度大小为g。

(1)当弹簧恢复原长时，P的速度大小；

(2)若Q的质量为m，求Q到达圆轨道最低点B时对轨道的压力；

(3)在第(2)问的基础上，Q能够到达D点吗？若能，求出到达D点时的速度；若不能，请说明理由。

Answer 1

【答案】(1) (2) (3)能，

【解析】

(1)在弹簧从压缩到恢复原长，设恢复原长时P物体的速度为，则根据功能关系：

所以解得：

(2)P与质量为m的物体Q发生弹性碰撞，设碰撞后P、Q的速度分别为、 ，则：

解得.

Q运动到B点时，设轨道对物体的支持力为F，则：

解得；根据牛顿第三定律，所以物体对轨道的压力为6mg

(3)设物体Q能通过D点，则过D点时最小速度为

而B到D的过程有：

解得.

因为：

所以能到达D点，且=

答：(1)当弹簧恢复原长时P的速度大小为；

(2)若Q的质量为m，Q到达圆轨道最低点B时对轨道的压力为；

(3)在第(2)问的基础上Q能够到达D点，到达D点时的速度=.