题目内容
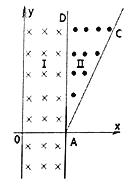
【题目】如图所示,扇形区域AOB内存在有垂直平面向内的匀强磁场,OA和OB互相垂直是扇形的两条半径,长度为R.一个带电粒子1从A点沿AO方向进入磁场,从B点离开,若与该粒子完全相同的带电粒子2以同样的速度从C点平行AO方向进入磁场,C到AO的距离为R/2,则下列说法错误的是()
A. 1粒子从B点离开磁场时,速度方向沿OB方向 B. 粒子带正电
C. 2粒子仍然从B点离开磁场 D. 两粒子在磁场中运动时间之比为4:3
【答案】D
【解析】
由粒子可以进入磁场,得到在A点的偏转方向,进而得到电荷符号;再根据粒子速度方向及粒子运动的两点得到粒子运动半径,进而得到出射点及偏转角度,从而得到运动时间之比。
带电粒子从A点沿AO方向进入磁场,从B点离开,那么粒子在A点向右上方偏转,则由左手定则可判定粒子带正电,故B说法正确;粒子1从A点正对圆心射入,恰从B点射出,粒子在磁场中运动的圆心角为90°,1粒子从B点离开磁场时,速度方向沿OB方向,故A说法正确;粒子2以同样的速度从C点平行AO方向进入磁场轨迹如图所示:
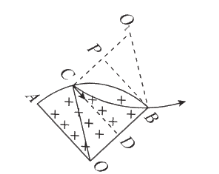
设对应的圆心为O1,运动的轨道半径也为BO=R,连接O1C、O1B,O1COB是平行四边形,O1B=CO,则粒子2一定从B点射出磁场,故C说法正确;粒子1的速度偏转角![]() ,连接PB,可知P为O1C的中点,由数学知识可知
,连接PB,可知P为O1C的中点,由数学知识可知![]() ,粒子在磁场中运动的周期为:
,粒子在磁场中运动的周期为:![]() ,两粒子的周期相等,粒子在磁场中运动时间:
,两粒子的周期相等,粒子在磁场中运动时间:![]() ,运动时间之比:
,运动时间之比:![]() ,故D说法错误。所以选D。
,故D说法错误。所以选D。

练习册系列答案
相关题目