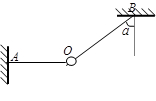题目内容
(16分)如图所示,轻杆两端分别系着质量为 的圆环A和质量为
的圆环A和质量为 的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为
的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为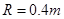 m的1/4圆弧。质量为
m的1/4圆弧。质量为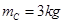 的小球C以
的小球C以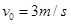 的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取
的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取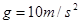 ,则:
,则:

(1)碰后C球平抛的水平位移 (2)碰后瞬间B球的速度 (3)A、B间轻杆的长度
 的圆环A和质量为
的圆环A和质量为 的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为
的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为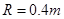 m的1/4圆弧。质量为
m的1/4圆弧。质量为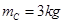 的小球C以
的小球C以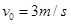 的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取
的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取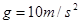 ,则:
,则:
(1)碰后C球平抛的水平位移 (2)碰后瞬间B球的速度 (3)A、B间轻杆的长度
(1)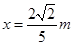 (2)
(2)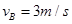 (3)
(3)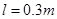
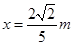 (2)
(2)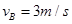 (3)
(3)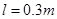
试题分析: (1)碰后C球恰好能做平抛运动,则C球在圆弧顶端,由牛顿第二定律:
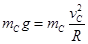
水平方向:
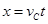
竖直方向:
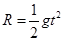
解得:
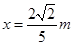
(2)碰撞过程中,B球和C球组成的系统动量守恒:
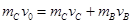
解得:
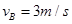
(3)碰后当B球恰好与横杆接触时,二者具有相同的水平速度v共。
水平方向动量守恒
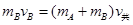
系统机械能守恒
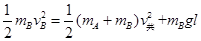
解得:
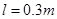

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
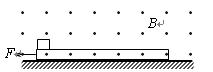




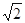 m/s可以使小球不脱离轨道
m/s可以使小球不脱离轨道
 ,则小球能够上升的最大高度等于R/2
,则小球能够上升的最大高度等于R/2 ,则小球能够上升的最大高度小于3R/2
,则小球能够上升的最大高度小于3R/2 ,则小球能够上升的最大高度等于2R
,则小球能够上升的最大高度等于2R ,则小球能够上升的最大高度等于2R
,则小球能够上升的最大高度等于2R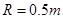 的光滑半圆轨道竖直固定在高
的光滑半圆轨道竖直固定在高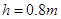 的光滑水平台上,与平台平滑连接,平台长
的光滑水平台上,与平台平滑连接,平台长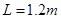 .可视为质点的两物块
.可视为质点的两物块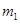 、
、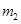 束缚在一起,并静止在平台的最右端D点,它们之间有被压缩的轻质弹簧,某时刻突然解除束缚,使两物块
束缚在一起,并静止在平台的最右端D点,它们之间有被压缩的轻质弹簧,某时刻突然解除束缚,使两物块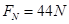 ,水平抛出后在水平地面上的落在水平地面上的P点,
,水平抛出后在水平地面上的落在水平地面上的P点,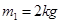 ,
,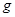 取
取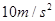 .求:
.求: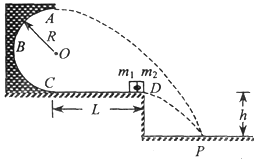
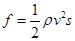 ,式中ρ为大气的密度,v是返回舱的运动速度,s为与形状特征有关的阻力面积。当返回舱距地面高度为10km时打开面积为1200m2的降落伞,直到速度达到8m/s后匀速下落。为实现软着陆(即着陆时返回舱的速度为零),当返回舱离地面1.2m时反冲发动机点火,使返回舱落地的速度减为零,返回舱此时的质量为2.7×103kg。(取g=10m/s2)
,式中ρ为大气的密度,v是返回舱的运动速度,s为与形状特征有关的阻力面积。当返回舱距地面高度为10km时打开面积为1200m2的降落伞,直到速度达到8m/s后匀速下落。为实现软着陆(即着陆时返回舱的速度为零),当返回舱离地面1.2m时反冲发动机点火,使返回舱落地的速度减为零,返回舱此时的质量为2.7×103kg。(取g=10m/s2)