题目内容
如图所示,半径r=0.8m的光滑圆轨道被竖直固定在水平地面上,圆轨道最低处有一质量为0. 4kg的小球(小球的半径比r小很多)。现给小球一个水平向右的初速度v0,下列关于在小球的运动过程中说法正确的是(g取10m/s2)( )


| A.v0≤4m/s可以使小球不脱离轨道 |
B.v0≥4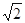 m/s可以使小球不脱离轨道 m/s可以使小球不脱离轨道 |
| C.设小球能在圆轨道中做完整的圆周运动,在最低点与最高点对轨道的压力之差为24N |
| D.设小球能在圆轨道中做完整的圆周运动,在最低点与最高点对轨道的压力之差为20N |
AC
试题分析: 要使小球不脱离轨道运动,1、越过最高点.2、不越过四分之一圆周;最高点的临界情况mg=
 解得v=
解得v=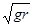 =
=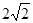 m/s;根据机械能守恒定律得,
m/s;根据机械能守恒定律得,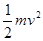 +mg?2r=
+mg?2r=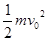 ,解得v0=
,解得v0=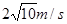 ;若不通过四分之一圆周,根据机械能守恒定律有: mgr=
;若不通过四分之一圆周,根据机械能守恒定律有: mgr=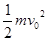 ,解得v0=
,解得v0=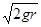 =4m/s。故小球不脱离轨道,v0<4m/s或v0>
=4m/s。故小球不脱离轨道,v0<4m/s或v0>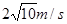 ,故A对,B错;若小球能在圆轨道中做完整的圆周运动,在最高点,由向心力公式:FN1+mg=
,故A对,B错;若小球能在圆轨道中做完整的圆周运动,在最高点,由向心力公式:FN1+mg=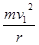 ,在最低点,由向心力公式:FN2-mg=
,在最低点,由向心力公式:FN2-mg=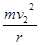 ,
,由根据机械能守恒定律得,mg?2r
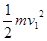 =
=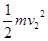 ,得FN2- FN2=24N,故C正确,D错误
,得FN2- FN2=24N,故C正确,D错误
练习册系列答案
相关题目



 ,其中r为该点到Q的距离(选无限远的电势为零)。求液珠能到达的最高点B离A点的高度
,其中r为该点到Q的距离(选无限远的电势为零)。求液珠能到达的最高点B离A点的高度 。
。
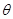 ,车和人的总质量为
,车和人的总质量为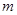 ,做圆周运动的半径为
,做圆周运动的半径为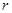 ,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )
,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )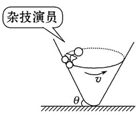
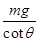
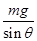
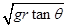
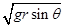
 的圆环A和质量为
的圆环A和质量为 的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为
的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为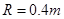 m的1/4圆弧。质量为
m的1/4圆弧。质量为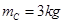 的小球C以
的小球C以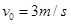 的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取
的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取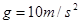 ,则:
,则: