题目内容
长度为0.2m的轻质细杆OA，A端有一质量为1kg的小球，以O点为圆心，在竖直平面内做圆周运动，如图所示，小球通过最高点时的速度为2m/s，取g=10m/s2，则此时轻杆OA将（ ）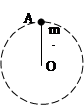
| A．受到10N的拉力 |
| B．受到10N的压力 |
| C．受到20N的拉力 |
| D．受到20N的压力 |
A
解析试题分析：小球在细杆的作用下，在竖直平面内做圆周运动．小球到达最高点时，受重力和杆的弹力，先假设为向下的弹力，杆的弹力和重力的合力提供向心力，由牛顿第二定律得：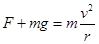
解得：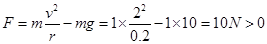
故弹力的方向与假设的方向相同，为向下的10N拉力．
根据牛顿第三定律，球对杆有向上的10N拉力．故选A．
考点：本题主要考查对向心力来源的分析以及牛顿第二定律和牛顿第三定律的简单应用．
津桥教育计算小状元系列答案
mg的恒力F向上拉B，当运动距离为h时B与A分离。下列说法正确的是（ ）
下列有关运动的说法正确的是：（ ）
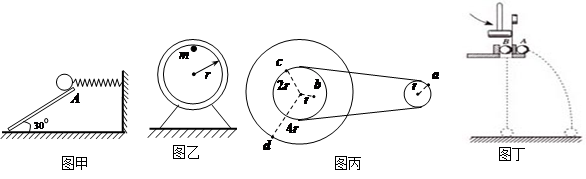
| A．图甲中撤掉挡板A的瞬间，小球的加速度竖直向下 |
| B．图乙中固定在竖直面内的圆环内径r=1.6m，小球沿内圆表面过最高点速度可以为2m/s |
| C．图丙中皮带轮上b点的加速度小于a点的加速度 |
| D．图丁中用铁锤水平打击弹簧片后，B球比A球先着地 |
如图所示，用相同材料做成的质量分别为m1、m2的两个物体中间用一轻弹簧连接。在下列四种情况下，相同的拉力F均作用在m1上，使m1、m2作加速运动：①拉力水平，m1、m2在光滑的水平面上加速运动。②拉力水平，m1、m2在粗糙的水平面上加速运动。③拉力平行于倾角为θ的斜面，m1、m2沿光滑的斜面向上加速运动。④拉力平行于倾角为θ的斜面，m1、m2沿粗糙的斜面向上加速运动。以△l1、△l2、△l3、△l4依次表示弹簧在四种情况下的伸长量，则有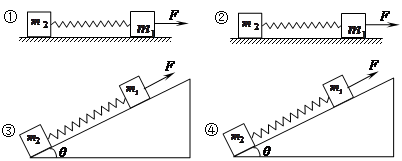
| A．△l2＝△l4 | B．△l4＞△l3 |
| C．△l1＞△l3 | D．△l2＞△l1 |
利用传感器和计算机可以测量快速变化的力的瞬时值。实验时，把小球举高到弹性绳子的悬点O 处，然后放手让小球自由下落。图是用这种方法获得的弹性绳中拉力随时间的变化图线。由图所提供的信息，以下正确的是( )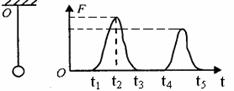 
| A．t2时刻小球速度最大 |
| B．小球和弹性绳组成的系统机械能不守恒 |
| C．t1到t2期间小球速度一直减小到零 |
| D．t1到t2期间小球重力势能减少量小于弹性绳弹性势能增加量 |
，试求两物块的加速度大小和方向；
，试求两物块的加速度大小和方向；
，试求两物块的加速度大小和方向。如图5所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力．已知AP＝2R，重力加速度为g，则小球从P到B的运动过程中 
| A．重力做功2mgR | B．机械能减少mgR | C．合外力做功mgR | D．克服摩擦力做功 mgR |
如图所示，小物块从光滑的倾斜轨道上的Ｐ点自由滑下，到达底端后滑上一水平传送带（轨道底端与传送带表面相齐平）。当传送带静止时，小物块通过传送带后水平飞出落到地面上，物块与皮带因摩擦产生的热量为Q。当皮带轮按逆时针方向匀速转动时，则小物块从Ｐ点自由滑下后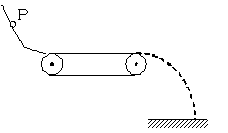
| A．有可能滑不到传送带右端 |
| B．能通过传送带，但落点会变得近一些 |
| C．能通过传送带，但摩擦产生的热量大于Q |
| D．能通过传送带，但物体克服摩擦力做的功大于Q |
如图所示，细线的一端系一质量为m的小球，另一端固定在倾角为θ的光滑斜面体顶端，细线与斜面平行．在斜面体以加速度a水平向右做匀加速直线运动的过程中，小球始终静止在斜面上，重力加速度为g，小球受到细线的拉力为T，斜面的支持力为FN，则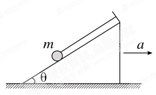
| A．T＝m(g sinθ＋a cosθ) |
| B．T＝m(g cosθ＋a sinθ) |
| C．FN＝m(g cosθ－a sinθ) |
| D．FN＝m(g cosθ＋a sinθ) |