题目内容
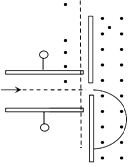
【题目】如图所示,传送带与水平面间的夹角θ=37,沿顺时针匀速转动.现把质量m=50kg的米袋轻轻放在底端A,并输送到顶端B,A、B间的距离L=20m.可以认为最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2 , sin37=0.6,cos37=0.8.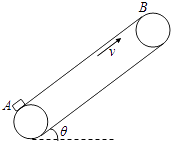
(1)要使米袋能够被输送到传送带顶端,米袋与传送带间动摩擦因数应满足什么条件?
(2)若米袋与传送带间动摩擦因数μ=0.8,且米袋一直向上做匀加速直线运动,则米袋到达传送带顶端B时的速度vB多大?
(3)若米袋与传送带间动摩擦因数μ=0.8,改变传送带的速度大小v,可以调节米袋到达传送带顶端B的时间t,试写出t随v变化的关系式.
【答案】
(1)解:要使米袋能够被输送到传送带顶端B,则应有:μmgcosθ≥mgsinθ
代入数据解得:μ≥0.75
答:要使米袋能够被输送到传送带顶端,米袋与传送带间动摩擦因数应满足的条件是:μ≥0.75.
(2)解:当μ=0.8,则米袋一直向上做匀加速直线运动,米袋到达传送带顶端B的过程,由动能定理得:
![]()
代入数据解得:vB=4m/s
答:米袋到达传送带顶端B时的速度vB是4m/s.
(3)解:由(2)可知,当传送带速度v<4m/s时,米袋先加速至传送带的速度v,然后随传送带一起匀速运动.设米袋加速运动时的位移为x,加速度为a,则
根据牛顿第二定律得:μmgcosθ﹣mgsinθ=ma
由运动学公式有:v2=2ax
米袋运动的时间为: ![]() (或 4vt﹣5v2﹣80=0)
(或 4vt﹣5v2﹣80=0)
当传送带速度v≥4m/s时,米袋一直做匀加速运动,则米袋运动的时间恒为: ![]()
答:t随v变化的关系式是 4vt﹣5v2﹣80=0.
【解析】(1)要使米袋能够被输送到传送带顶端,最大静摩擦力应大于等于重力沿斜面向下的分力,由此列式求解.(2)米袋做匀加速直线运动,由动能定理求米袋到达传送带顶端B时的速度vB.(3)根据米袋速度与传送带速度的关系,分析米袋的运动情况,由牛顿第二定律和运动学公式结合解答.