题目内容
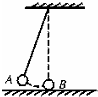
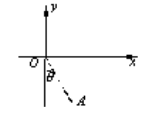
将带正电量Q="0.3" C，质量m′="0.15" kg的滑块，放在小车的绝缘板的右端，小车的质量M="0.5" kg，滑块与绝缘板间的动摩擦因数μ=0.4，小车的绝缘板足够长，它们所在的空间存在着磁感应强度B="2.0" T的水平方向的匀强磁场，开始时小车静止在光滑水平面上，当一个摆长为L="1.25" m，摆球质量m="0.4" kg的单摆从水平位置由静止释放，摆到最低点时与小车相撞，如图所示，碰撞后摆球恰好静止，g取10 m/s2.求：
（1）小车碰撞后瞬间的速度是多少？
（2）摆球与小车碰撞过程中系统损失的机械能△E是多少？
（3）碰撞后小车的最终速度是多少？
（1）小车碰撞后瞬间的速度是多少？
（2）摆球与小车碰撞过程中系统损失的机械能△E是多少？
（3）碰撞后小车的最终速度是多少？
（1）V=4m/s（2）△E=1J（3）V=3.25m/s
试题分析：（1）小球下落到最低点时的速度为
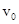，根据动能定理可得：
，解得
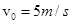，小球与小车碰撞过程中，动量守恒，故有：
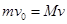，解得：
所以小车碰撞后瞬间的速度V=4m/s（2）小车和小球碰撞过程中损失的机械能为：
，带入数据可得
，（3）假设m′最终能与M一起运动，由动量守恒定律得：
，解得
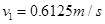
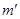以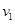
速度运动时受到的向上洛仑兹力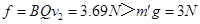
所以
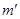在还未到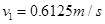时已与M分开了．由上面分析可知当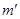的速度为
时便与M分开了，根据动量守恒定律可得方程：
解得
点评：要求同学们能根据求解需要选择不同的过程运动机械能守恒定律和动量守恒定理，难度较大．
练习册系列答案
相关题目
