题目内容
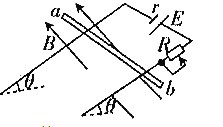
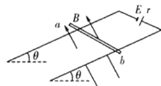
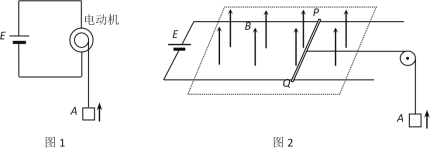
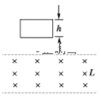
【题目】如图所示,两根平行粗糙金属导轨固定于绝缘水平面上,导轨左侧间连有阻值为r的电阻,两平行导轨间距为L。一根长度大于L、质量为m、接入电路的电阻也为r的导体棒垂直导轨放置并接触良好,导体棒初始均处于静止,导体棒与图中虚线有一段距离,虚线右侧存在竖直向上、磁感应强度为B的匀强磁场。现给导体棒一个水平向右的恒力,使其从静止开始做匀加速直线运动,进入磁场前加速度大小为a0,然后进入磁场,运动一段时间后达到一个稳定速度,平行轨道足够长,导体棒与平行导轨间的动摩擦因数处处相等,忽略平行轨道的电阻。求:
(1)导体棒最后的稳定速度大小;
(2)若导体棒从开始运动到达稳定速度的过程中,通过导轨左侧电阻的电荷量为q,求此过程中导体棒在磁场中运动的位移。

【答案】(1)vm=![]() (2)x=
(2)x=![]()
【解析】
(1)设水平恒力为F,导体棒到达图中虚线处速度为v,在进入磁场前,由牛顿运动定律有:
F-μmg=ma0
导体棒进入磁场后,导体棒最后的稳定速度设为vm,由平衡条件有:
F-μmg-![]() =0
=0
联立上面各式,得:
vm=![]()
(2)导体棒从进入磁场到达稳定速度的过程中,运动的位移设为x,由法拉第电磁感应定律有:
![]()
![]()
q=![]()
联立解得:
x=![]()

练习册系列答案
相关题目