��Ŀ����
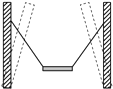
����Ŀ����ͼ��ʾ������ ![]() Բ������̶���ˮƽ�����ϣ��뾶R��ͬ��A����ɽ��������Ƴɣ�B����ɽ���Բ���Ƴɣ�������Ϊ�⻬�������������Ҳ�����Ϸ��ֱ���С��A��B�ɾ�ֹ�ͷţ�С��������ĸ߶ȷֱ���hA��hB��ʾ��������˵����ȷ���ǣ� ��
Բ������̶���ˮƽ�����ϣ��뾶R��ͬ��A����ɽ��������Ƴɣ�B����ɽ���Բ���Ƴɣ�������Ϊ�⻬�������������Ҳ�����Ϸ��ֱ���С��A��B�ɾ�ֹ�ͷţ�С��������ĸ߶ȷֱ���hA��hB��ʾ��������˵����ȷ���ǣ� ��
A.��hA=hB=2R������С�����ع���˶�����ߵ�
B.��hA=hB= ![]() �����ڻ�е���غ㣬��С���ڹ�����������߶�Ϊ
�����ڻ�е���غ㣬��С���ڹ�����������߶�Ϊ ![]()
C.�ʵ�����hA��hB �� ����ʹ��С��ӹ����ߵ�ɳ���ǡ�����ڹ���Ҷ˿ڴ�
D.��ʹС���ع���˶����Ҵ���ߵ�ɳ���AС�����С�߶�Ϊ ![]() ��BС����С�߶�Ϊ2R
��BС����С�߶�Ϊ2R
���𰸡�D
���������⣺A��D��С��Aǡ���ܵ�A�������ߵ�ʱ����mg=m ![]() ��vA=
��vA= ![]() �����ݻ�е���غ㶨�ɵã�mg��hA��2R��=
�����ݻ�е���غ㶨�ɵã�mg��hA��2R��= ![]() �����hA=
�����hA= ![]() R����С��Bǡ���ܵ�B�������ߵ�ʱ������ߵ���ٶ�vB=0�����ݻ�е���غ㶨�ɵ�hB=2R���ɼ���hA=2Rʱ��A���ܵ���������ߵ㣮��A����D��ȷ��
R����С��Bǡ���ܵ�B�������ߵ�ʱ������ߵ���ٶ�vB=0�����ݻ�е���غ㶨�ɵ�hB=2R���ɼ���hA=2Rʱ��A���ܵ���������ߵ㣮��A����D��ȷ��
B����hB= ![]() ʱ��B��������ߵ�ʱ�ٶ�Ϊ0��С��B�ڹ�������������߶ȵ���
ʱ��B��������ߵ�ʱ�ٶ�Ϊ0��С��B�ڹ�������������߶ȵ��� ![]() ʱ����hA=hB=
ʱ����hA=hB= ![]() ʱ��С��A�ڵ�����ߵ�ǰ�뿪�������һ�����ٶȣ��ɻ�е���غ��֪��A�ڹ�������������߶�С��hB=
ʱ��С��A�ڵ�����ߵ�ǰ�뿪�������һ�����ٶȣ��ɻ�е���غ��֪��A�ڹ�������������߶�С��hB= ![]() ����B����
����B����
C��С��A����ߵ�ɳ�����ƽ���˶�������R�߶�ʱ��ˮƽλ�Ƶ���СֵΪxA=vA ![]() =
= ![]()
![]() =
= ![]() R��R������С��A���ڹ���Ҷ˿���࣮���ʵ�����hB �� B�������ڹ���Ҷ˿ڴ��������ʵ�����hA��hB �� ֻ��B��ӹ����ߵ�ɳ���ǡ�����ڹ���Ҷ˿ڴ�����C����
R��R������С��A���ڹ���Ҷ˿���࣮���ʵ�����hB �� B�������ڹ���Ҷ˿ڴ��������ʵ�����hA��hB �� ֻ��B��ӹ����ߵ�ɳ���ǡ�����ڹ���Ҷ˿ڴ�����C����
��ѡD
�����㾫���������������ͻ�е���غ㼰�������ǽ����ĸ�������Ҫ֪������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ������������ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ��䣮